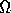In order to formulate the equations governing turbulent flow in general coordinates, tensor notation will be used; for an introduction see [Aris, 1962].
The physical domain with curved boundaries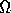 
is transformed to a rectangle
G with the mapping
Here, 
are Cartesian coordinates and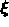 
are
boundary conforming curvilinear coordinates. The mapping is assumed to be
regular, i.e. the Jacobian of the transformation does not vanish. Covariant
base vectors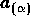 
, contravariant base vectors
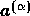, and the covariant and contravariant metric tensors
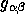and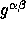 
are defined as
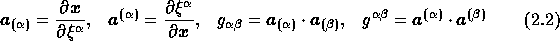
The square root of the determinant of the covariant metric tensor, denoted by
, equals the Jacobian of the transformation. The following formulae for
covariant derivatives of tensors of rank zero, one and two, respectively, are
used in this paper:
where
is the Christoffel symbol of the second kind. The summation convention holds for Greek indices.
Turbulent flow is governed by the continuity equation and the Reynolds-averaged
Navier-Stokes equations. The Reynolds stresses are related to the mean rates of
strain through the isotropic eddy-viscosity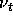 
, which is calculated by the
standard high-Re k-
model [Launder and Spalding, 1974].
The tensor formulation of these equations is given by
where 
is the contravariant mean velocity component, p is the
pressure, 
is the kinematic viscosity,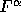 
is an external
force per unit volume, k is the turbulent kinetic energy, 
is the
turbulent energy dissipation rate and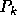 
is the production of turbulent
energy, given by
Finally,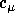 
, 
, 
, 
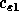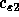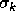and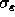 
are
dimensionless constants which, respectively, are taken to be 0.09, 1.44, 1.92,
1.0 and 1.3. The values of these constants are recommended in
[Launder and Spalding, 1974].
Specification of the boundary conditions is straightforward, except in near-wall regions where wall functions are adopted to avoid integration through the viscous sublayer and to obtain log-layer solutions [Launder and Spalding, 1974]. These wall functions are given by:
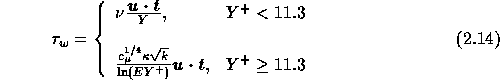
where
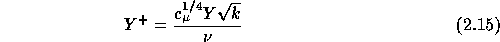
and
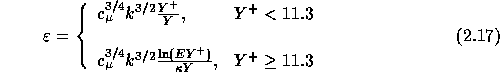
Here,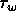 
is the wall shear stress, Y is the distance perpendicular to the
wall, 
is the Von Kármán constant (
0.4) and E is a
roughness parameter, approximately equal to 
for a smooth wall.
The quantity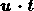 
denotes the tangential velocity along the
wall and is given by
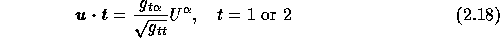
Finally, the flux of turbulent energy through the wall is set to zero and the
value of 
at the first grid point away from the wall is determined from
