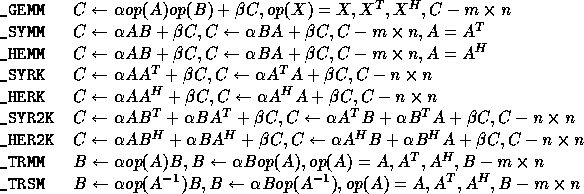next up previous contents
Next: Source developing and Up: Programming and documentation standards Previous: Example

BLAS-subroutines

  By Lawson, Hanson, Kincaid and Krogh a number of basic linear algebra subroutines have been proposed (ACM Tans, Math, Software 5, 3 (Sept. 1979), 308-323) which are generally accepted as the so-called BLAS subroutines. In most vector computers efficient implementations of these subroutines are available, which fully utilize the vectorial and parallel properties of these computers. Besides that the source of these subroutines is available so that they can be implemented at any other computer. In 1985 respectively 1988 the level two and three BLAS-subroutines have been introduced.
The level 1 BLAS-subroutines have the following tasks: (level 1):


Next we give a quick reference guide for the BLAS level 1, 2 en 3 subroutines.
Meaning of prefixes 

     S - REAL                C - COMPLEX
     D - DOUBLE PRECISION    Z - COMPLEX*16
                             (may not be supported
                              by all machines)
For the Level 2 BLAS a set of extended-precision routines with the prefixes ES, ED, EC, EZ may also be available.

Level 1 BLAS


In addition to the listed routines there are two further extended-precision dot product routines DQDOTI and DQDOTA.

Level 2 and Level 3 BLAS
Matrix types

GE - GEneral     GB - General Band
SY - SYmmetric   SB - Sym. Band     SP - Sym. Packed
HE - HErmitian   HB - Herm. Band    HP - Herm. Packed
TR - TRiangular  TB - Triang. Band  TP - Triang. Packed

Level 2 and Level 3 BLAS
Options


Dummy options arguments are declared as CHARACTER1 and may be passed as character strings. 
 
TRANS_ 		 = 		 `No transpose', `Transpose',


              		   		 `Conjugate transpose' ()


UPLO   		 = 		 `Upper triangular', `Lower triangular'


DIAG   		 = 		 `Non-unit triangular', `Unit triangular'


SIDE   		 = 		 `Left', `Right' (A or op(A) on the left,


              		   		  or A or op(A) on the right)
For real matrices, TRANS_=`T' and TRANS_=`C' have the same meaning.
For Hermitian matrices, TRANS_=`T' is not allowed.
For complex symmetric matrices, TRANS_=`H' is not allowed.

References


C. Lawson, R. Hanson, D. Kincaid, and F. Krogh, ``Basic Linear Algebra Subprograms for Fortran Usage,'' ACM Trns. on Math. Soft. 5(1979) 308-325
J.J. Dongarra, J. DuCroz, S. Hammarling, and R. Hanson, ``An Extended Set of Fortran Basic Linear Algebra Subprograms,'' ACM Trans. on Math. Soft. 14, 1(1988) 1-32
J.J. Dongarra, J. DuCroz, I. Duff, and S. Hammarling, ``A Set of Level 3 Basic Linear Algebra Subprograms,'' ACM Trans. on Math. Soft. (Dec. 1989)

Obtaining the Software via netlib@mcs.anl.gov


To receive the real single-precision software, in the mail message type 
     send sblas from blas
     send sblas2 from blas
     send sblas3 from blas
To receive the real double-precision software, in the mail message type 
     send dblas from blas
     send dblas2 from blas
     send dblas3 from blas
To receive the complex single-precision software, in the mail message type 
     send cblas from blas
     send cblas2 from blas
     send cblas3 from blas
To receive the complex double-precision software, in the mail message type 
     send zblas from blas
     send zblas2 from blas
     send zblas3 from blas

Level 1 BLAS

                  dim scalar vector   vector   scalars              5-element array   prefixes
SUBROUTINE _ROTG (                                     A, B, C, S )                   S, D
SUBROUTINE _ROTMG(                             D1, D2, A, B,        PARAM )           S, D
SUBROUTINE _ROT  ( N,        X, INCX, Y, INCY,               C, S )                   S, D
SUBROUTINE _ROTM ( N,        X, INCX, Y, INCY,                      PARAM )           S, D
SUBROUTINE _SWAP ( N,        X, INCX, Y, INCY )                                       S, D, C, Z
SUBROUTINE _SCAL ( N, ALPHA, X, INCX )                                                S, D, C, Z, CS, ZD
SUBROUTINE _COPY ( N,        X, INCX, Y, INCY )                                       S, D, C, Z
SUBROUTINE _AXPY ( N, ALPHA, X, INCX, Y, INCY )                                       S, D, C, Z
FUNCTION   _DOT  ( N,        X, INCX, Y, INCY )                                       S, D, DS
FUNCTION   _DOTU ( N,        X, INCX, Y, INCY )                                       C, Z
FUNCTION   _DOTC ( N,        X, INCX, Y, INCY )                                       C, Z
FUNCTION   __DOT ( N,        X, INCX, Y, INCY )                                       SDS
FUNCTION   _NRM2 ( N,        X, INCX )                                                S, D, SC, DZ
FUNCTION   _ASUM ( N,        X, INCX )                                                S, D, SC, DZ
FUNCTION   I_AMAX( N,        X, INCX )                                                S, D, C, Z
Explanation

Level 2 BLAS

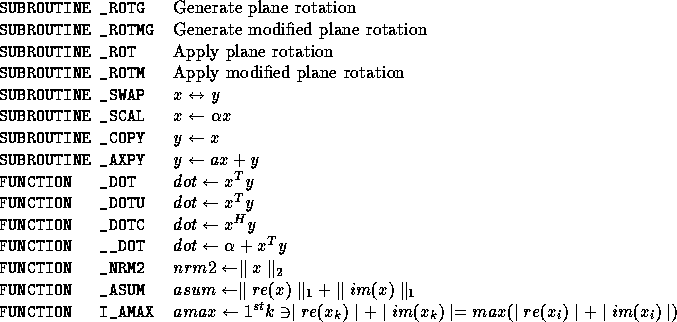
       options             dim   b-width scalar matrix  vector  scalar vector     prefixes
_GEMV (       TRANS,       M, N,         ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  S, D, C, Z
_GBMV (       TRANS,       M, N, KL, KU, ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  S, D, C, Z
_HEMV ( UPLO,                 N,         ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  C, Z
_HBMV ( UPLO,                 N, K,      ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  C, Z
_HPMV ( UPLO,                 N,         ALPHA, AP,     X, INCX, BETA, Y, INCY )  C, Z
_SYMV ( UPLO,                 N,         ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  S, D
_SBMV ( UPLO,                 N, K,      ALPHA, A, LDA, X, INCX, BETA, Y, INCY )  S, D
_SPMV ( UPLO,                 N,         ALPHA, AP,     X, INCX, BETA, Y, INCY )  S, D
_TRMV ( UPLO, TRANS, DIAG,    N,                A, LDA, X, INCX )                 S, D, C, Z
_TBMV ( UPLO, TRANS, DIAG,    N, K,             A, LDA, X, INCX )                 S, D, C, Z
_TPMV ( UPLO, TRANS, DIAG,    N,                AP,     X, INCX )                 S, D, C, Z
_TRSV ( UPLO, TRANS, DIAG,    N,                A, LDA, X, INCX )                 S, D, C, Z
_TBSV ( UPLO, TRANS, DIAG,    N, K,             A, LDA, X, INCX )                 S, D, C, Z
_TPSV ( UPLO, TRANS, DIAG,    N,                AP,     X, INCX )                 S, D, C, Z
Explanation

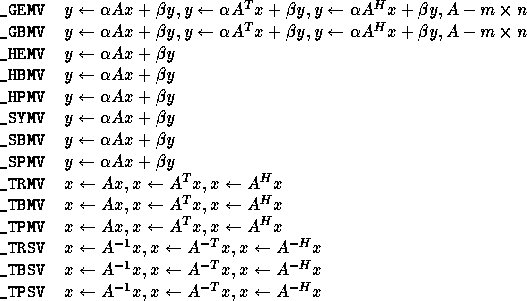
       options             dim   scalar vector   vector   matrix    prefixes
_GER  (                    M, N, ALPHA, X, INCX, Y, INCY, A, LDA )  S, D
_GERU (                    M, N, ALPHA, X, INCX, Y, INCY, A, LDA )  C, Z
_GERC (                    M, N, ALPHA, X, INCX, Y, INCY, A, LDA )  C, Z
_HER  ( UPLO,                 N, ALPHA, X, INCX,          A, LDA )  C, Z
_HPR  ( UPLO,                 N, ALPHA, X, INCX,          AP )      C, Z
_HER2 ( UPLO,                 N, ALPHA, X, INCX, Y, INCY, A, LDA )  C, Z
_HPR2 ( UPLO,                 N, ALPHA, X, INCX, Y, INCY, AP )      C, Z
_SYR  ( UPLO,                 N, ALPHA, X, INCX,          A, LDA )  S, D
_SPR  ( UPLO,                 N, ALPHA, X, INCX,          AP )      S, D
_SYR2 ( UPLO,                 N, ALPHA, X, INCX, Y, INCY, A, LDA )  S, D
_SPR2 ( UPLO,                 N, ALPHA, X, INCX, Y, INCY, AP )      S, D
Explanation


Level 3 BLAS

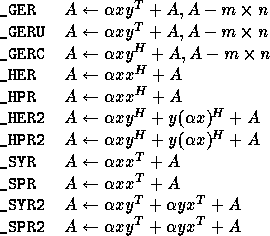
       options                            dim      scalar matrix  matrix  scalar matrix    prefixes
_GEMM (             TRANSA, TRANSB,       M, N, K, ALPHA, A, LDA, B, LDB, BETA,  C, LDC )  S, D, C, Z
_SYMM ( SIDE, UPLO,                       M, N,    ALPHA, A, LDA, B, LDB, BETA,  C, LDC )  S, D, C, Z
_HEMM ( SIDE, UPLO,                       M, N,    ALPHA, A, LDA, B, LDB, BETA,  C, LDC )  C, Z
_SYRK (       UPLO, TRANS,                   N, K, ALPHA, A, LDA,         BETA,  C, LDC )  S, D, C, Z
_HERK (       UPLO, TRANS,                   N, K, ALPHA, A, LDA,         BETA,  C, LDC )  C, Z
_SYR2K(       UPLO, TRANS,                   N, K, ALPHA, A, LDA, B, LDB, BETA,  C, LDC )  S, D, C, Z
_HER2K(       UPLO, TRANS,                   N, K, ALPHA, A, LDA, B, LDB, BETA,  C, LDC )  C, Z
_TRMM ( SIDE, UPLO, TRANSA,         DIAG, M, N,    ALPHA, A, LDA, B, LDB )                 S, D, C, Z
_TRSM ( SIDE, UPLO, TRANSA,         DIAG, M, N,    ALPHA, A, LDA, B, LDB )                 S, D, C, Z
Explanation


next up previous contents
Next: Source developing and Up: Programming and documentation standards Previous: Example


ISNaS ontwikkeling
Wed May 24 08:37:14 METDST 1995