De methode van Newton-Raphson

Prof.dr.ir. C. Vuik
Technische Universiteit Delft
e-mail: c.vuik@tudelft.nl

De methode van Newton-Raphson is een numerieke methode om het nulpunt van een functie te bepalen. We zullen de methode uitleggen aan de hand van het volgende probleem: gegeven de functie f bepaal het nulpunt p zodanig dat f(p) = 0.
Stel p0 is een benadering van het nulpunt p. Maak nu de raaklijn h(x) aan f door het punt (p0,f(p0)). De formule van h is:

h(x) = f(p0) + df
dx
 (p0) (x-p0).
Om een nieuwe (betere) benadering te vinden van p bepalen we p1, die het nulpunt is van h, dus h(p1) = 0. Invullen geeft:
0 = f(p0) + df
dx
 (p0) (p1-p0).
Als we nu p1 naar links brengen en alle andere termen naar rechts, dan krijgen we (onder de voorwaarde dat [(df)/(dx)](p0) is ongelijk aan 0):
p1 = p0 - f(p0)
df
dx
 (p0)
 .
Zo kunnen we doorgaan om p2, p3, ... te vinden. De procedure staat uitgelegd in het onderstaande plaatje.



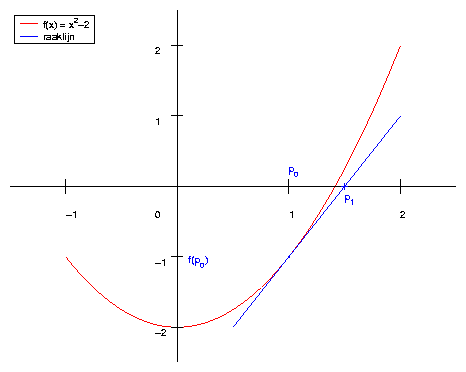
Figuur: De Newton-Raphson methode

Voorbeeld
Stel we willen het positieve nulpunt bepalen van de functie f(x) = x2-2. Het exacte antwoord in 6 decimalen is 1.41421. We nemen als startpunt p0 = 1. De vergelijking van de raaklijn is nu

h(x) = -1 + 2(x-1).
De nieuwe benadering van het nulpunt p1 is nu:
p1 = 1 - -1
2
 = 1.5.
Zo doorgaande vinden we:
p1 = 1.50000
p2 = 1.41666
p3 = 1.41421
Hieruit blijkt dat de oplossing al na 3 stappen gevonden is.