Numerical methods
Examples
Rounding errors
In general it is difficult to get a good analysis of rounding errors
due to floating point arithmetic done by computers. To motivate the
study of rounding errors we note that several
disasters are originated by rounding errors. Recent examples are:
Patriot Missile Failure and the
Explosion of the Ariane 5.
Rounding errors can also has important political and/or economical
consequences. Examples are
the index of The Vancouver Stock Exchange ,
the conversion to Euro's,
and
Rounding error changes Parliament makeup.
Numerical errors
The sinking of the
Sleipner A offshore platform has been caused by
inaccurate finite element approximation of the linear elastic model of the
tricell (using the popular finite element program NASTRAN).
The shear stresses were underestimated by 47%, leading to insufficient
design.
Double pendulum
As an application of the theory given in Chapter 5 of this course a
simulation (using a Java-applet) of a double pendulum is possible.
The integration
is done by a Runge-Kutta method.
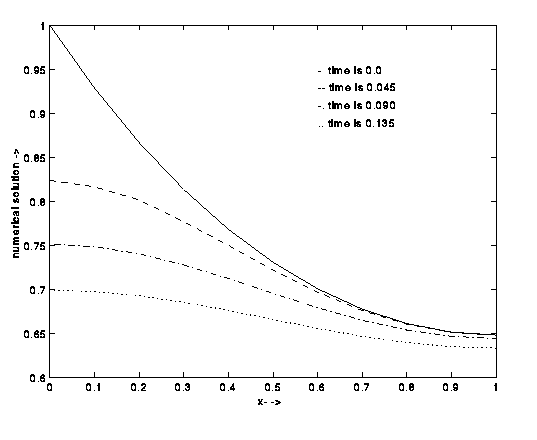
Heat equation
In Chapter 6 of this course the numerical methods are applied
to approximate the solution of the heat equation. There are many
practical examples, which can be described by the heat equation.
One of them is the diffusion of oxygen in the skin. In some radio
therapies the best results are obtained if the oxygen concentration
is as low as possible. The outer surface of the skin is sealed off
and the concentration decreases, due to the fact that the skin
uses the oxygen at a certain rate. For different times the
concentration profiles are calculated and given in the
figure below:
Here is an animation of the concentration
profiles
Contact information:
Kees Vuik
Back to
educational page or
home page
of Kees Vuik

