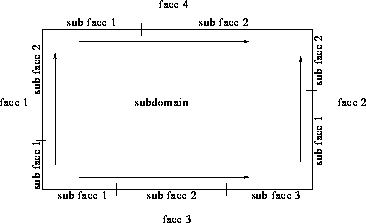
Figure 10: Directions and numbering of faces and sub faces
The itopol array stores the connections between the blocks. The basic idea behind the itopol data-structure is that the blocks communicate through common sub-faces. For instance in 2-D, each block consists of four faces numbered 1--4. The faces are divided into sub faces that are numbered from west to east and from south to north, see Fig. 10. The itopol array stores for each sub face the neighbouring block (0 if the sub face is external) and the corresponding neighbouring face and subface numbers. This means that:

Figure 10: Directions and numbering of faces and sub faces
A sub face in 2-D is described by the index range 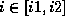 where i denotes the number of a grid cell not the number of grid points.
Because in a general 3-D case the sub faces may have complex shapes which
are hard to represent, we restrict the shape of the sub faces:
where i denotes the number of a grid cell not the number of grid points.
Because in a general 3-D case the sub faces may have complex shapes which
are hard to represent, we restrict the shape of the sub faces:
In 3-D sub faces consist of grid cells in a rectangular index rangeIn 3-D, the itopol array possibly needs some extensions because sharing of sub faces is not enough to completely determine the coupling between blocks.
The itopol array consists of three parts:
- Pos. 1
- nblocks
- Pos. 2
- nfaces (= 2*ndim)
- Pos. 3
- maxnsubfaces (maximum number of subfaces encountered on all faces)
- Pos. 4
- lensubface (current number of integers stored for each subface in the subfaces array)
- Pos. 5
- Start address of Part II
of this array
- Pos. 6
- Start address of Part III
of this array
Part II is of length nblocks*nfaces and stores the nsubfaces array:integer nsubfaces(1:nblocks, 1:nfaces)The value nsubfaces(i,j) is the number of subfaces at face j of block i.
Part III stores the actual multi-block topology in the subfaces array:In 3-D, the iorient field is not yet defined and always 0. In 2-D, the iorient field is computed based on the following three quantities:integer subfaces(1:nblocks, 1:nfaces, 1:maxnsubfaces, 1:lensubface)The value subfaces(i,j,k,m) is the value of position m of the subface record for sub face k of face j of block i. The subface record is organized as follows:
- Pos. 1
- i1 (lower i index of sub face)
- Pos. 2
- i2 (upper i index of sub face)
- Pos. 3
- j1 (lower j index of sub face)
- Pos. 4
- j2 (upper j index of sub face)
- Pos. 5
- blockno (number of neighbouring block)
- Pos. 6
- faceno (number of neighbouring face number)
- Pos. 7
- subfaceno (number of neighbouring sub face number)
- Pos. 8
- iorient (relative orientation of the blocks)
 between this
block and its neighbour. This quantity is used in combination
with nsign to determine the sign change when
copying normal fluxes:
between this
block and its neighbour. This quantity is used in combination
with nsign to determine the sign change when
copying normal fluxes:  .
relblockor=0 means no sign change, 1 means a sign change.
.
relblockor=0 means no sign change, 1 means a sign change.
