The discretization of the transport equation (5.1) as explained in the
previous section is restricted to more or less smooth grids. Moreover,
the diffusion coefficient 
often varies rapidly, so that
has large jumps on cell faces. Hence, straightforward
discretization
of the diffusivity may results in large errors even on smooth grids. Here we shall
consider a discretization which is exact for uniform and linear scalar fields,
regardless the smoothness of the grid and of the diffusion coefficient.
For this purpose, we need an expression for the partial derivative of any quantity
with respect to 
in terms of general coordinates, namely
This can be derived using the chain rule and (2.27). We start with the equation (5.1), viz.,
and with (5.7) taken into account, the appropriate form of the transport equation becomes
Discretization of (5.9) is obtained by integration over a finite
volume 
with center (i,j,k).
Hence, we have
whereas the time derivative and the source terms are integrated using the midpoint rule:
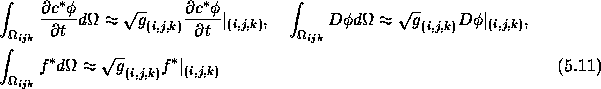
So far, no difficulties arose because none of the quantities used in the above
formulae are discontinuous. Furthermore, these discretizations are second order
accurate and (5.10) is exact for constant 
.
The cell-face values have to be approximated in terms of values of in
neighbouring cell centers by means of interpolation. This will be discussed in
the next section.
The only point left to discuss is the approximation of the diffusion term.
First, for the sake of easier manipulations, the diffusion term will hereafter
be expressed as
Integration over yields:
The physical quantity 
is everywhere continuous for
arbitrary mappings. Hence, when k is
discontinuous, 
is discontinuous. Thus, approximation of
using central differences is inaccurate. However, using the
integration-path method an accurate approximation of
at point (i+1/2,j,k), for example, is obtained:
where
where C is given by
and
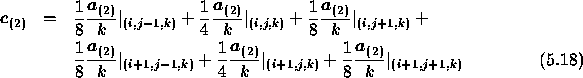
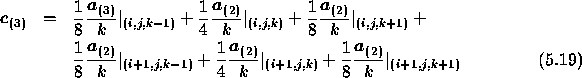
We hereby assume that 
.
The two-dimensional version of (5.15) and (5.16) are given by
with
Substitution of (5.14) in (5.13) gives a discretization which
is exact when is constant, and hence exact for linear scalar fields.
The other cell-face fluxes can be derived in exactly the similar way.
