Two-equation eddy-viscosity models are based on approximate constitutive equations
which predict the unknown Reynolds stress tensor ![]() that appears
in the Reynolds-averaged Navier-Stokes equations (4.1).
Through the introduction of a turbulent viscosity
that appears
in the Reynolds-averaged Navier-Stokes equations (4.1).
Through the introduction of a turbulent viscosity ![]() these models relate
these models relate
![]() to mean flow variables. The most popular eddy-viscosity model
is due to Boussinesq. He postulated that in analogy to molecular diffusion, the
Reynolds stresses depend on the deformation rates of the mean flow as follows:
to mean flow variables. The most popular eddy-viscosity model
is due to Boussinesq. He postulated that in analogy to molecular diffusion, the
Reynolds stresses depend on the deformation rates of the mean flow as follows:
where k is the turbulent kinetic energy per unit mass, defined as
The term ![]() has been added to ensure that
the trace of equation (6.1) produces identical expressions on either side
of the equality sign. Furthermore, this term can be absorbed by the pressure
gradient term. We then have to replace static pressure by
has been added to ensure that
the trace of equation (6.1) produces identical expressions on either side
of the equality sign. Furthermore, this term can be absorbed by the pressure
gradient term. We then have to replace static pressure by
![]() . Expressions similar to (6.1) are employed for
the turbulent fluxes of heat and mass which are counterparts of Fourier's and
Fick's laws for the respective molecular fluxes. The turbulent diffusivities of
heat and mass that result are then related directly to
. Expressions similar to (6.1) are employed for
the turbulent fluxes of heat and mass which are counterparts of Fourier's and
Fick's laws for the respective molecular fluxes. The turbulent diffusivities of
heat and mass that result are then related directly to ![]() through constant
turbulent Prandtl/Schmidt numbers, which are empirically determined and are of
the order of unity. The eddy-viscosity
through constant
turbulent Prandtl/Schmidt numbers, which are empirically determined and are of
the order of unity. The eddy-viscosity ![]() is predicted from the solution of
two semi-empirical transport equations for two turbulence quantities to be
presented later.
is predicted from the solution of
two semi-empirical transport equations for two turbulence quantities to be
presented later.
Although the Boussinesq hypothesis works quite well for many flows (i.e. two-dimensional flows), it is too simplistic. More specifically, it assumes that turbulent diffusion is isotropic, so that primary shear stresses will be predicted well, but not secondary shear stresses and normal stresses. As a result the Boussinesq hypothesis may not be suitable for difficult flows involving strong three-dimensional effects. This weakness can potentially be removed using anisotropic eddy-viscosity models. The idea is to extend the stress-strain relationship (6.1) by adding nonlinear elements of the mean velocity gradient tensor. This leads to better approximations of the normal and shear stresses and therefore turbulence anisotropy structure.
Based on series-expansion arguments (details may be found in [7]), a general and coordinate-invariant quadratic relationship between stresses and strains can be written as
where ![]() ,
, ![]() ,
, ![]() and
and
![]() are the contravariant and covariant components of the
mean rate of strain and rotation tensors, respectively, viz.,
are the contravariant and covariant components of the
mean rate of strain and rotation tensors, respectively, viz.,
![]()
![]()
Note that the quadratic products of strain and rotation tensors are grouped so
that the resultant is symmetric in ![]() and
and ![]() . Approach has been to
determine the closure coefficients
. Approach has been to
determine the closure coefficients ![]() ,
, ![]() ,
, ![]() and
and
![]() so that agreement is achieved with a simple shear flow and with one
other difficult class of flow. Several researchers have proposed anisotropic
eddy-viscosity models (AEVM). These models in the current version of ISNaS
include: the nonlinear AEVM of Speziale [29], the RNG based nonlinear
AEVM of Rubinstein and Barton [21], the nonlinear variant of Nisizima and
Yoshizawa arising from the Kraichnan's DIA theory [19] and the
anisotropic eddy-viscosity closure of Myong and Kasagi [18].
Although the theoretical origins and derivations of these eddy-viscosity models
differ greatly, they can be cast into a common mathematical form,
like (6.3). They merely differ in respect of the numerical values of the
closure constants, as given in Table 6.1.
so that agreement is achieved with a simple shear flow and with one
other difficult class of flow. Several researchers have proposed anisotropic
eddy-viscosity models (AEVM). These models in the current version of ISNaS
include: the nonlinear AEVM of Speziale [29], the RNG based nonlinear
AEVM of Rubinstein and Barton [21], the nonlinear variant of Nisizima and
Yoshizawa arising from the Kraichnan's DIA theory [19] and the
anisotropic eddy-viscosity closure of Myong and Kasagi [18].
Although the theoretical origins and derivations of these eddy-viscosity models
differ greatly, they can be cast into a common mathematical form,
like (6.3). They merely differ in respect of the numerical values of the
closure constants, as given in Table 6.1.
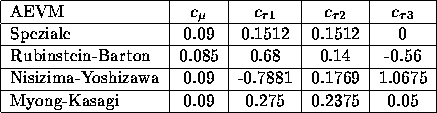
Table 6.1: Numerical values of closure constants in stress-strain relation.
It should be noted that the Boussinesq hypothesis is obtained by setting
![]() ,
, ![]() and
and ![]() to zero.
to zero.
The turbulent viscosity ![]() must be specified by the two-equation model.
Two-equation models are turbulence models in which the evolution of both the
velocity and length scales characterizing turbulent motion is obtain by solving
semi-empirical partial differential equations. At the moment four two-equation
models are dealt with: the standard k-
must be specified by the two-equation model.
Two-equation models are turbulence models in which the evolution of both the
velocity and length scales characterizing turbulent motion is obtain by solving
semi-empirical partial differential equations. At the moment four two-equation
models are dealt with: the standard k- ![]() model of Launder and
Spalding [15], the RNG based k-
model of Launder and
Spalding [15], the RNG based k- ![]() variant of
Yakhot et al. [40], the extended k-
variant of
Yakhot et al. [40], the extended k- ![]() model of Chen
and Kim [3] and Wilcox's k-
model of Chen
and Kim [3] and Wilcox's k- ![]() closure [38].
closure [38].
If the k- ![]() modeling framework is employed, the turbulent viscosity
is related to k and
modeling framework is employed, the turbulent viscosity
is related to k and ![]() , the dissipation rate of k, through the
following semi-empirical expression:
, the dissipation rate of k, through the
following semi-empirical expression:
![]()
where k and ![]() are determined from the coordinate-invariant
semi-empirical transport equations
are determined from the coordinate-invariant
semi-empirical transport equations
![]()
where ![]() is the production rate of turbulent energy given by
is the production rate of turbulent energy given by
Different variants of the above model arise from the different approaches to
determining the model coefficients ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() . The coefficient
. The coefficient
![]() is made a function of the equilibrium state of turbulence
which is characterizes by the ratio of times scales of turbulence and mean strain,
denoted as
is made a function of the equilibrium state of turbulence
which is characterizes by the ratio of times scales of turbulence and mean strain,
denoted as ![]() . Here
. Here
![]() is the magnitude of
the mean rate of strain. It should be noted that if the production rate of
turbulent energy (6.9) is modeled using the Boussinesq hypothesis, then
we obtain a simple expression for
is the magnitude of
the mean rate of strain. It should be noted that if the production rate of
turbulent energy (6.9) is modeled using the Boussinesq hypothesis, then
we obtain a simple expression for ![]() , namely
, namely
![]() . In the above three k-
. In the above three k- ![]() models
models ![]() is obtained as follows:
is obtained as follows:

where ![]() and
and ![]() .
The numerical values used in the three k-
.
The numerical values used in the three k- ![]() variants for the closure
constants are tabulated below.
variants for the closure
constants are tabulated below.
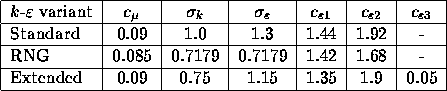
Table 6.2: Numerical values of closure constants in k- ![]() closure.
closure.
The extended model in ISNaS employs slightly revised values for coefficients
![]() and
and ![]() . Chen and Kim [3]
recommended
. Chen and Kim [3]
recommended ![]() and
and ![]() which
produce significantly wrong solutions over a wide range of flows. In [8],
it was reported that this model give consistently better results, when
which
produce significantly wrong solutions over a wide range of flows. In [8],
it was reported that this model give consistently better results, when
![]() and
and ![]() .
.
The three k- ![]() variants are of the high-Reynolds-number type and the
viscosity-affected near wall region is resolved with a low-Reynolds-number model
according to Lam and Bremhorst [14]. An alternative and still widely
employed approach is the use of so-called wall functions. This issue will be
presented in Section 7. When the low-Reynolds-number k-
variants are of the high-Reynolds-number type and the
viscosity-affected near wall region is resolved with a low-Reynolds-number model
according to Lam and Bremhorst [14]. An alternative and still widely
employed approach is the use of so-called wall functions. This issue will be
presented in Section 7. When the low-Reynolds-number k- ![]() model is
used the values of the closure constants
model is
used the values of the closure constants ![]() ,
, ![]() ,
,
![]() ,
, ![]() and
and ![]() remain the same and the viscous
damping functions are introduced into the constants, as follows:
remain the same and the viscous
damping functions are introduced into the constants, as follows:
![]()
The damping functions are chosen according to the model proposed by Lam and Bremhorst [14]:
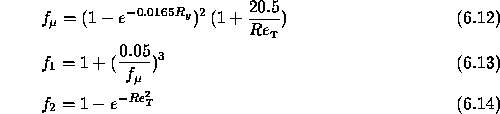
with
![]()
the local and turbulent Reynolds numbers, respectively.
Furthermore, Y is the normal distance to the solid boundary.
Boundary conditions for the momentum, k and ![]() equations are,
respectively,
equations are,
respectively,
![]()
For computational expediency, we choose
as the boundary condition for the dissipation rate, as suggested by Lam and Bremhorst [14]. The disadvantage of the low-Reynolds-number models is that they impose a very fine mesh normal to the wall, which can be prohibitive when dealing with large 3D applications.
Many proposals for the k- ![]() model have been made (for a review, see
[39]). The version devised by Wilcox [38] is perhaps the most
popular one and will be presented here. Rather than solving for the dissipation
rate of turbulent energy, the second variable considered here is the specific
dissipation rate, i.e. the rate of dissipation per unit kinetic energy. This
variable is denoted as
model have been made (for a review, see
[39]). The version devised by Wilcox [38] is perhaps the most
popular one and will be presented here. Rather than solving for the dissipation
rate of turbulent energy, the second variable considered here is the specific
dissipation rate, i.e. the rate of dissipation per unit kinetic energy. This
variable is denoted as ![]() .
On the basis of a simple dimensional analysis, the eddy-viscosity is taken
to be the quotient of the turbulent energy and the specific dissipation rate,
thus:
.
On the basis of a simple dimensional analysis, the eddy-viscosity is taken
to be the quotient of the turbulent energy and the specific dissipation rate,
thus:
![]()
The two turbulent parameters obey the following modeled transport equations:
![]()
![]()
where ![]() is given by (6.9). The closure constants employed are as
follows:
is given by (6.9). The closure constants employed are as
follows:
The k- ![]() model is a low-Reynolds-number closure which means that it can be
integrated through the viscous sub-layer without requiring a near-wall model.
Hence, standard boundary conditions must be employed at a solid wall, i.e. for the
momentum equations noslip conditions are imposed on the boundary and k is simply
zero on the wall. Due to the singular behaviour of
model is a low-Reynolds-number closure which means that it can be
integrated through the viscous sub-layer without requiring a near-wall model.
Hence, standard boundary conditions must be employed at a solid wall, i.e. for the
momentum equations noslip conditions are imposed on the boundary and k is simply
zero on the wall. Due to the singular behaviour of ![]() at the wall, a special
boundary condition for
at the wall, a special
boundary condition for ![]() must be used, which is given by
must be used, which is given by
where
The singularity at Y=0 does not allow this boundary condition to be imposed on the wall. The numerical treatment of this singularity will be presented in the next section.
For stagnation flows, the so-called Kato-Launder modification [10], which replaces the strain in the production of turbulent energy term by the vorticity, has been implemented. Using the Boussinesq eddy-viscosity approximation, we obtain
In a stagnation flow, the very high levels of S produce excessive levels of
turbulent energy whereas deformation near stagnation point is nearly irrotational.
Defining the magnitude of the mean rotation as
![]() and replacing
(6.24) by
and replacing
(6.24) by
leads to a marked reduction in energy production near the stagnation point, while having no effect in a simple shear flow [10]. In [2] a hybrid form is proposed in which (6.24) and Kato-Launder correction (6.25) are averaged:
![]()
with ![]() a weight factor. This hybrid model is particularly
used for stagnation flows. In that case the weight factor is chosen to be
a weight factor. This hybrid model is particularly
used for stagnation flows. In that case the weight factor is chosen to be
![]() , as recommended by [2].
, as recommended by [2].