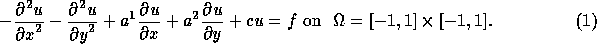
For the solution of the incompressible Navier-Stokes equations in domains of arbitrary shape, we use a block-structured finite volume method is used. References [20,9,27] describe the discretization in detail and reference [21] discusses the capability of the method to accurately solve a number of benchmark problems. A Schwarz type domain decomposition iteration in combination with a GMRES [23] acceleration is used to solve the resulting domain decomposition problem. Significant reductions in computing time can be obtained using the GMRES acceleration procedure, see [5] and [4].
However, since this method requires an accurate solution of subdomains, the computing time can be much larger than with single block solution for the same number of unknowns. Another problem with this method is that it is not known beforehand how accurate the subdomains must be solved. A possible solution to both problems is to solve the linear equations on the subdomains inaccurately. The effect of this is that the GMRES acceleration procedure can no longer be used because the preconditioner may vary in each iteration. Instead, a method based on GCR [14] is used. For the special case of a single domain, this method simplifies to GMRESR [24] if GMRES is used to solve the subdomains (inaccurately).
Theoretical analysis of the effect of inaccurate solution of subdomains seems intractable. Therefore we take recourse to numerical experiments. We compare some results on solving the subdomains accurately and inaccurately for a two-dimensional model problem, namely the advection-diffusion equation:
This equations is a good model of what can be expected when the method is
applied to the momentum equations in Navier-Stokes solution methods.
With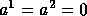 
we obtain a Poisson equation which is a good model
for the pressure equation occurring in the pressure-correction method.
A cell-centered discretization is used, see [5] for details on
domain decomposition and discretization for this equation.
The results are reported in the entire range between
very accurate subdomain solution with tolerance
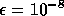and very inaccurate solution using a blocked version of
the subdomain ILU postconditioner.
In the literature, much focus is on parallel algorithms. However, parallel implementations are not immediately available and one can imagine situations where parallel execution is not (efficiently) possible. Therefore, to obtain an efficient sequential domain decomposition algorithm we pay much attention to multiplicative domain decomposition. The prospects for parallel implementation are also discussed.
