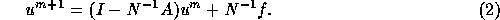
The basic Schwarz domain decomposition iteration converges slowly because, for practical reasons, in computation fluid dynamics minimal overlap is usually used. Therefore, some acceleration procedure for this iterative procedure is needed. Krylov subspace methods are frequently used to accelerate domain decomposition methods, see for example [1] and many of the papers on iterative substructuring methods in [15,7,8,16,19]. This section presents both the acceleration procedure used with accurate solution of subdomains and the procedure used with inaccurate solution of subdomains.
Basically, the domain decomposition iteration is of the following form
with A the global discretization matrix over all domains and
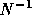 an approximation to the inverse of the block diagonal or
block lower-diagonal matrix of A. The matrix N is called the
block Jacobi and Gauss-Seidel matrix of A respectively.
The matrix A is divided into blocks where each block corresponds with
all unknowns in a single subdomain.
For instance, for a decomposition into 3 blocks
we have
an approximation to the inverse of the block diagonal or
block lower-diagonal matrix of A. The matrix N is called the
block Jacobi and Gauss-Seidel matrix of A respectively.
The matrix A is divided into blocks where each block corresponds with
all unknowns in a single subdomain.
For instance, for a decomposition into 3 blocks
we have
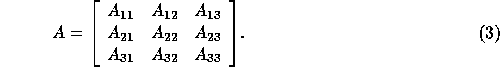
In [5] we assumed that the subdomains were
solved accurately so that 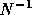 is the exact inverse of the
block diagonal or block lower-diagonal matrix of A, so
is the exact inverse of the
block diagonal or block lower-diagonal matrix of A, so
with 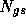 the Gauss-Seidel version and
the Gauss-Seidel version and
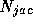 the Jacobi version of N.
The Gauss-Seidel version is suitable for implementation on a single
processor and leads to the sequential or multiplicative algorithm.
The Jacobi version is suitable for parallelization and is called
the parallel or additive version.
the Jacobi version of N.
The Gauss-Seidel version is suitable for implementation on a single
processor and leads to the sequential or multiplicative algorithm.
The Jacobi version is suitable for parallelization and is called
the parallel or additive version.
It can be
seen that the left-hand side of (2) only depends on the
values of 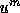 near an interface. This means that if we split the
vector u into vectors w en v with w the non-interface unknowns
and v the interface unknowns, see Figure 1, we have
near an interface. This means that if we split the
vector u into vectors w en v with w the non-interface unknowns
and v the interface unknowns, see Figure 1, we have
with 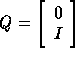 an injection operator from v into
an injection operator from v into
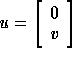 .
From (5), it follows that
.
From (5), it follows that 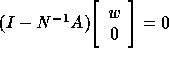 so that the
non-interface unknowns do not contribute to the computation of
so that the
non-interface unknowns do not contribute to the computation of
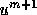 in (2).
in (2).
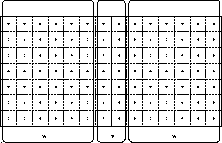
Figure 1: Interface variables v and non-interface variables w for
a 5-point discretization stencil and a decomposition into
two blocks
By substituting (5) into (2) and by premultiplying with
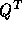 we get
we get
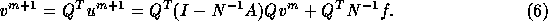
Since we are interested in the stationary solution v of this iteration process we get
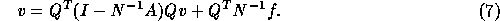
which is equivalent to
Therefore, accurate solution of subdomains finally leads to a system concerning only the interface equations. Accelerated domain decomposition in [5] amount to solving the interface equations (8) using GMRESR [24]. The required matrix-vector product can be computed by doing one domain decomposition iteration, see [5] for details.
Inaccurate solution of subdomains implies that we no longer take the
exact inverse of N but use some approximation 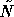 to N, so
to N, so
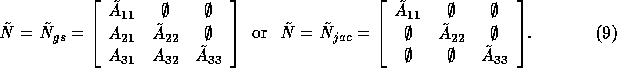
with 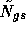 the Gauss-Seidel (sequential) version and
the Gauss-Seidel (sequential) version and
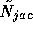 the Jacobi (parallel) version of
the Jacobi (parallel) version of 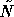 .
In the literature, much focus is on parallel algorithms. However,
parallel implementations are not immediately available and one
can imagine situations where parallel execution is not possible.
Suppose for instance that there is only one workstation to do computations
on. Therefore, to obtain an efficient sequential domain decomposition
algorithm we pay much attention the the Gauss-Seidel version of N.
.
In the literature, much focus is on parallel algorithms. However,
parallel implementations are not immediately available and one
can imagine situations where parallel execution is not possible.
Suppose for instance that there is only one workstation to do computations
on. Therefore, to obtain an efficient sequential domain decomposition
algorithm we pay much attention the the Gauss-Seidel version of N.
The matrix vector product of 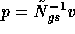 is computed like
is computed like
Here 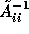 represents the approximate solution in
subdomain i up to a low accuracy using GMRES. A special case occurs when we
take
represents the approximate solution in
subdomain i up to a low accuracy using GMRES. A special case occurs when we
take 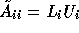 to be some incomplete LU factorization
of
to be some incomplete LU factorization
of 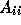 . This paper also investigates this case for ILUD factorization,
see further on.
. This paper also investigates this case for ILUD factorization,
see further on.
The GMRES subdomain solution implicitly constructs a polynomial 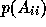 of the subdomain matrix
of the subdomain matrix 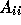 such that the final residual
such that the final residual
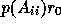 is minimal in the
is minimal in the 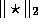 norm. Specifically, with
initial guess
norm. Specifically, with
initial guess 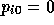 and right-hand side
and right-hand side 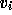 , we get for the final
subdomain solution
, we get for the final
subdomain solution 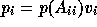 .
Since the polynomial,
.
Since the polynomial, 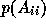 depends on both the required accuracy
and the right-hand side (initial residual), the matrix
depends on both the required accuracy
and the right-hand side (initial residual), the matrix
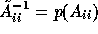 can be different for each v.
Therefore, the GMRES acceleration procedure cannot be used since
the preconditioner
can be different for each v.
Therefore, the GMRES acceleration procedure cannot be used since
the preconditioner 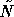 varies in each step.
varies in each step.
The GCR [14] method can be easily adapted to cope with
variable preconditioners. Because of its simplicity and for
completeness, we derive the GCR
method here. The GCR method is based on maintaining two
subspaces, a subspace 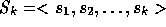 for storing the
search directions
for storing the
search directions 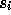 and a subspace
and a subspace
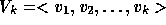 with
with 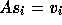 . In every operation
of GCR the property
. In every operation
of GCR the property 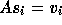 is preserved.
The GCR method minimizes the residual
is preserved.
The GCR method minimizes the residual
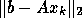 over
over 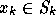 . Clearly, if the
. Clearly, if the 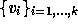 form an orthonormal basis, we can obtain the solution by projecting onto
the space
form an orthonormal basis, we can obtain the solution by projecting onto
the space 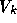 . So we must find
. So we must find 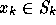 such that
such that
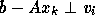 for
for 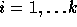 , therefore,
, therefore,
Since 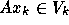 we have
we have
and by substituting (12)
into (11)
we get 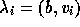 so that
so that

Since 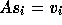 , we have
, we have
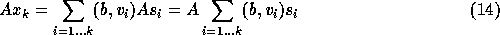
so that 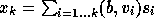 .
This gives
.
This gives 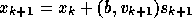 and
with
and
with 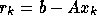 we get
we get
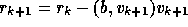 .
The GCR algorithm proceeds by choosing a new search direction
.
The GCR algorithm proceeds by choosing a new search direction 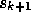 (preferably such that
(preferably such that 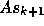 approximates the residual
approximates the residual 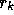 ) and computes the vector
) and computes the vector
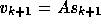 . A modified Gram-Schmidt procedure is used to
make
. A modified Gram-Schmidt procedure is used to
make 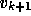 orthogonal to
orthogonal to 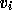 (
(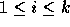 ). The same linear
combinations of vectors are applied to the space of search directions
). The same linear
combinations of vectors are applied to the space of search directions 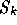 to ensure that
to ensure that 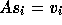 still holds for all i.
Figure 2 shows the resulting GCR algorithm.
still holds for all i.
Figure 2 shows the resulting GCR algorithm.

Figure 2: The GCR algorithm with general search directions without
restart and with a relative stopping criterion [24]
For the special case of the search direction 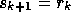 , we
obtain the classical GCR algorithm, which is equivalent to GMRES [23].
For this choice of search direction, the space
, we
obtain the classical GCR algorithm, which is equivalent to GMRES [23].
For this choice of search direction, the space 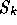 is called the
Krylov space. The difference between GCR and GMRES is that, at the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and
is called the
Krylov space. The difference between GCR and GMRES is that, at the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and 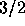 times the number of floating
point operations for orthogonalization.
However GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [17] strategy,
whereas GMRES can only be restarted. Because of this, GCR may converge
faster than GMRES.
times the number of floating
point operations for orthogonalization.
However GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [17] strategy,
whereas GMRES can only be restarted. Because of this, GCR may converge
faster than GMRES.
Recent developments have led to a more flexible GMRES algorithm which allows more general search directions, so called FGMRES [22]. Also, the amount of work in GCR can be reduced to approximately that of GMRES if restarted GCR is used, see [25]. The resulting algorithm is comparable to FGMRES both in memory requirements and work. The GCR method achieves the same goal as FGMRES in a more understandable way.
The present paper considers only restarted GCR to compare with subdomain solution (which uses restarted GMRES). The optimizations of [25] are not used in this paper but will certainly be considered for domain decomposition for the incompressible Navier-Stokes equations.
If we compute the search direction 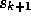 using some GMRES iterations
for solving
using some GMRES iterations
for solving 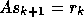 we obtain the GMRESR [24] algorithm.
In the present paper, we use
we obtain the GMRESR [24] algorithm.
In the present paper, we use 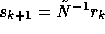 .
If the subdomains are solved (inaccurately) using GMRES, this method reduces
to GMRESR for the single domain case. If the subdomains are approximately
solved using
some ILU factorization we obtain a blocked version of the
subdomain ILU postconditioning called IBLU, which was investigated
for parallel implementation in (Incomplete Block
LU) [13,18,10,11]. In this paper we also investigate
the sequential version of IBLU.
For a single domain, this method is equivalent to GMRES with an ILU
postconditioner.
.
If the subdomains are solved (inaccurately) using GMRES, this method reduces
to GMRESR for the single domain case. If the subdomains are approximately
solved using
some ILU factorization we obtain a blocked version of the
subdomain ILU postconditioning called IBLU, which was investigated
for parallel implementation in (Incomplete Block
LU) [13,18,10,11]. In this paper we also investigate
the sequential version of IBLU.
For a single domain, this method is equivalent to GMRES with an ILU
postconditioner.
For the special case where 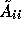 corresponds to
incomplete LU factorization,
the preconditioner is constant and the GMRES acceleration procedure may
also be applied. The only difference between the general method, based on
GCR, and the GMRES acceleration is that GMRES requires less vector updates
and less memory. Both methods of acceleration will be considered for IBLU
postconditioning.
corresponds to
incomplete LU factorization,
the preconditioner is constant and the GMRES acceleration procedure may
also be applied. The only difference between the general method, based on
GCR, and the GMRES acceleration is that GMRES requires less vector updates
and less memory. Both methods of acceleration will be considered for IBLU
postconditioning.
An important remark is that the stopping criterion for accurate solution
differs from that for inaccurate solution. With accurate solution,
the stopping criterion is based on the preconditioned residual
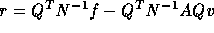 of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult since differences in computing time can
either be caused by a difference in convergence behavior or by the
difference in the definition of the residual. In this paper, we assume
that the difference in definition of the residual does not give different
accuracies of the final solution when using the relative stopping criterion
of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult since differences in computing time can
either be caused by a difference in convergence behavior or by the
difference in the definition of the residual. In this paper, we assume
that the difference in definition of the residual does not give different
accuracies of the final solution when using the relative stopping criterion
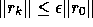 .
.