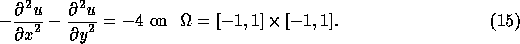
This section compares accurate with inaccurate solution of subdomains. Three problems are considered. The first is a Poisson equation
with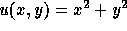 
on the boundary.
The second is a recirculating flow problem with oblique flow across the
interface:
with
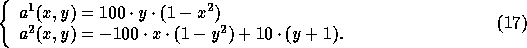
The term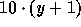 
makes the flow oblique across
vertical and horizontal interfaces. On the left and lower sides
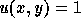is given and on the other sides 
holds.
This problem is known to be a difficult domain decomposition problem,
see [5].
A third problem is one with simple uniform flow:
with the same boundary conditions as problem two. Central discretization in space is applied.
The subdomains are solved using GMRES with ILUD preconditioning and a relative
stopping criterion. The subdomain solution accuracy is varied. As a special
case the subdomain solution is approximated by means of the inverse of the ILUD
preconditioner, see [12,26]. This preconditioner is of the form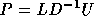 
with
L and U lower and upper triangular
matrices and D a diagonal matrix with
For a matrix with non-zero elements only on the positions
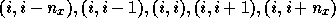this leads to
the recursion
with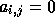 
if j is out of range. The ILUD preconditioner is
cheap in memory because only the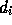 
for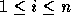 
need be stored
and it is also cheap in work.
The multi-block problem (the outer loop)
is solved up to a relative accuracy of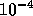 
.
In all experiments a Krylov space of dimension 20 is used for both
GMRES and GCR multi-block acceleration and for GMRES subdomain solution.
A restart after 20 iterations is used with both GMRES and GCR.
Iteration counts and computing times is given in the tables in the form itercount/time. The experiments were conducted on a HP9000/735 workstation.
In most of the experiments, the Gauss-Seidel (sequential) version of N is used. Only section 3.3 examines the possibilities for parallelism. Section 3.1 examines the effect of lowering the accuracy of the subdomain solution on the number of iterations and total computing time. Section 3.2 compares single block solution with multi-block solution with emphasis on the amount of additional time needed with multi-block (the multi-block penalty).
