


Next: Conclusions
Up: Results
Previous: Single domain versus
In this section, we take a brief look at the possibilities for parallel
implementation. Table 7 shows a comparison between the
block Gauss-Seidel and block Jacobi versions of the postconditioner 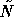 .
We see that the penalty of
going from the sequential to the parallel algorithm is approximately a
factor 2 if subdomains are solved inaccurately using GMRES.
With IBLUD postconditioning on the other hand, this factor is much less
than 2.
Also, computing time on
a single machine is minimized if IBLUD postconditioning is used.
This means that we expect good results from parallelization
of the IBLUD postconditioning.
.
We see that the penalty of
going from the sequential to the parallel algorithm is approximately a
factor 2 if subdomains are solved inaccurately using GMRES.
With IBLUD postconditioning on the other hand, this factor is much less
than 2.
Also, computing time on
a single machine is minimized if IBLUD postconditioning is used.
This means that we expect good results from parallelization
of the IBLUD postconditioning.
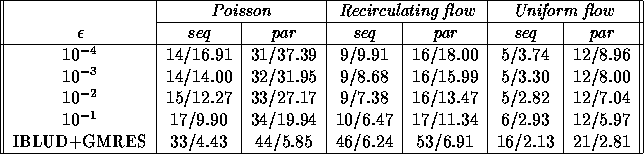
Table 7: Comparison between the sequential (Gauss-Seidel) and
parallel (Jacobi) version of the postconditioner 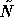 for
a decomposition into
for
a decomposition into 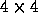 blocks.
blocks.
In [2,3] parallelization of domain decomposition for
the incompressible Navier-Stokes equations using accurate solution of
subdomains was investigated.
The method performed well on
a cluster of workstations. The reason was that with accurate solution
of subdomains the parallelization is rather coarse grained. Furthermore,
the reduction to a system of interface equations (8) made
a very simple implementation possible.
The results of the present study show, however, that with the algorithms
discussed in this paper,
the domain decomposition method on a single machine
will probably beat the current parallel implementation [2,3]
in the near future.
Parallelization of the algorithms of this report is also possible but involves
a parallelization of the GCR method itself.
As Table 7 shows, the number of iterations
increases only slightly as the subdomain solution accuracy is lowered to
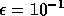 . Therefore, the communication overhead remains almost
constant while the amount of work decreases, which gives a lower computing
time (about a factor 2). The most efficient algorithm on a single
machine will probably not perform well on the cluster because then the
number of iterations is much larger which increases the communication
overhead significantly.
. Therefore, the communication overhead remains almost
constant while the amount of work decreases, which gives a lower computing
time (about a factor 2). The most efficient algorithm on a single
machine will probably not perform well on the cluster because then the
number of iterations is much larger which increases the communication
overhead significantly.



Next: Conclusions
Up: Results
Previous: Single domain versus
ISNaS ontwikkeling
Thu Jun 1 10:46:16 METDST 1995
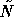 .
We see that the penalty of
going from the sequential to the parallel algorithm is approximately a
factor 2 if subdomains are solved inaccurately using GMRES.
With IBLUD postconditioning on the other hand, this factor is much less
than 2.
Also, computing time on
a single machine is minimized if IBLUD postconditioning is used.
This means that we expect good results from parallelization
of the IBLUD postconditioning.
.
We see that the penalty of
going from the sequential to the parallel algorithm is approximately a
factor 2 if subdomains are solved inaccurately using GMRES.
With IBLUD postconditioning on the other hand, this factor is much less
than 2.
Also, computing time on
a single machine is minimized if IBLUD postconditioning is used.
This means that we expect good results from parallelization
of the IBLUD postconditioning.

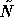 for
a decomposition into
for
a decomposition into 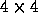 blocks.
blocks. 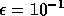 . Therefore, the communication overhead remains almost
constant while the amount of work decreases, which gives a lower computing
time (about a factor 2). The most efficient algorithm on a single
machine will probably not perform well on the cluster because then the
number of iterations is much larger which increases the communication
overhead significantly.
. Therefore, the communication overhead remains almost
constant while the amount of work decreases, which gives a lower computing
time (about a factor 2). The most efficient algorithm on a single
machine will probably not perform well on the cluster because then the
number of iterations is much larger which increases the communication
overhead significantly.