


Next: Single domain versus
Up: Results
Previous: Results
Table 1 lists the iteration counts and computation
times (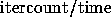 ) for the three problems.
The global grid consists of
) for the three problems.
The global grid consists of 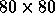 grid cells and it
was divided into
grid cells and it
was divided into 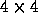 subdomains.
The first two rows concern the algorithm for accurate solution of
subdomains. The iteration counts for extremely accurate subdomain
solution with tolerance
subdomains.
The first two rows concern the algorithm for accurate solution of
subdomains. The iteration counts for extremely accurate subdomain
solution with tolerance 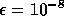 and
and 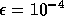 are the same.
From this we conclude that the subdomain solution accuracy with
tolerance
are the same.
From this we conclude that the subdomain solution accuracy with
tolerance 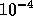 is accurate enough for this algorithm and test problem.
is accurate enough for this algorithm and test problem.
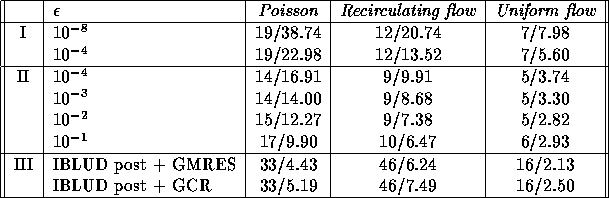
Table 1: Lowering the accuracy of subdomain solution. I is the algorithm
for accurate solution of subdomains, II for inaccurate solution
using GMRES, III is for IBLUD
The other rows are for the GCR based algorithm. Note that
in the special case of IBLUD postconditioning we have also listed
the more efficient GMRES acceleration.
As the subdomain solution accuracy is lowered the number of iterations
increases only slightly. Because of this the computing time drops
significantly for lower subdomain accuracies. Only for the special case of
IBLUD postconditioning, the number of iterations is significantly higher.
This rise in number of iterations does however not outweigh the reduction
in work by computing only 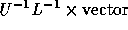 instead of doing GMRES. The computing
time with IBLUD postconditioning is by far the lowest. Note that the
amount of additional work in GCR acceleration compared to GMRES
acceleration can be significant. The only difference with GMRES is
that GCR needs some additional vector updates and requires some
more memory. A more efficient implementation, see [25], will
certainly be considered for the incompressible Navier-Stokes equations.
Mathematically,
the algorithms are the same for IBLUD postconditioning.
instead of doing GMRES. The computing
time with IBLUD postconditioning is by far the lowest. Note that the
amount of additional work in GCR acceleration compared to GMRES
acceleration can be significant. The only difference with GMRES is
that GCR needs some additional vector updates and requires some
more memory. A more efficient implementation, see [25], will
certainly be considered for the incompressible Navier-Stokes equations.
Mathematically,
the algorithms are the same for IBLUD postconditioning.
An important observation is that the GCR algorithm for inaccurate
solution of subdomains requires fewer iterations than the algorithm
for accurate subdomain solution using the same subdomain solution accuracy.
To show that this difference is not caused by the different definition of
the residual, we compare the computed solutions 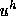 of the Poisson equation
with the exact solution
of the Poisson equation
with the exact solution 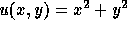 .
.
Table 2 shows
the maximum norms and 2-norms of the difference with the exact solution.
The 2-norm is defined as 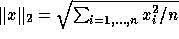 .
Clearly, the solutions obtained with both algorithms have approximately
the same accuracy. Only for large subdomain accuracy (giving very
large computing time) the algorithm for accurate solution of subdomains
gives a more accurate solution.
This verifies our earlier claim that the solution obtained with
GMRES acceleration used with accurate solution
of subdomains is sensitive to the subdomain solution accuracy.
This sensitivity is not present with the GCR based acceleration procedure
used with inaccurate solution of subdomains.
.
Clearly, the solutions obtained with both algorithms have approximately
the same accuracy. Only for large subdomain accuracy (giving very
large computing time) the algorithm for accurate solution of subdomains
gives a more accurate solution.
This verifies our earlier claim that the solution obtained with
GMRES acceleration used with accurate solution
of subdomains is sensitive to the subdomain solution accuracy.
This sensitivity is not present with the GCR based acceleration procedure
used with inaccurate solution of subdomains.
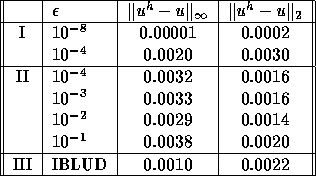
Table 2: Accuracy of the solution to the Poisson problem using
(I) the algorithm for accurate solution of subdomains,
(II) the algorithm for inaccurate solution of subdomains using
GMRES and
(III) for IBLUD
We see that with inaccurate solution of subdomains by ILUD (the IBLUD postconditioning),
we can reduce computing time is reduced
by a factor 2-6 compared to accurate solution
of subdomains.
In [6], a comparison between
accurate and inaccurate solution was made based on the number of iterations
only. This led to the conclusion that the simple accelerated
Schwarz algorithm using accurate subdomain solution was a competitive method
compared to single-domain ILU preconditioned GMRES.
The basis of analysis in the present paper is that we do less
work per iteration and therefore we allow some more iterations.
Therefore, although the number of iterations is machine and implementation
independent it should not be used as a basis for comparison.
Computing time is more suitable to compare algorithms but may give
different results depending on the implementation and machine architecture.
The most impressive reductions of computing time are obtained
for the Poisson equation, which is also the most expensive part of
the multi-block Navier-Stokes problem, see [4]. For the difficult
recirculating flow problem we obtain a reduction of a factor of 2. The
simpler uniform flow problem shows a reduction of a factor of 4.



Next: Single domain versus
Up: Results
Previous: Results
ISNaS ontwikkeling
Thu Jun 1 10:46:16 METDST 1995
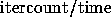 ) for the three problems.
The global grid consists of
) for the three problems.
The global grid consists of 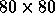 grid cells and it
was divided into
grid cells and it
was divided into 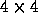 subdomains.
The first two rows concern the algorithm for accurate solution of
subdomains. The iteration counts for extremely accurate subdomain
solution with tolerance
subdomains.
The first two rows concern the algorithm for accurate solution of
subdomains. The iteration counts for extremely accurate subdomain
solution with tolerance 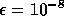 and
and 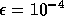 are the same.
From this we conclude that the subdomain solution accuracy with
tolerance
are the same.
From this we conclude that the subdomain solution accuracy with
tolerance 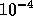 is accurate enough for this algorithm and test problem.
is accurate enough for this algorithm and test problem.

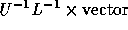 instead of doing GMRES. The computing
time with IBLUD postconditioning is by far the lowest. Note that the
amount of additional work in GCR acceleration compared to GMRES
acceleration can be significant. The only difference with GMRES is
that GCR needs some additional vector updates and requires some
more memory. A more efficient implementation, see [
instead of doing GMRES. The computing
time with IBLUD postconditioning is by far the lowest. Note that the
amount of additional work in GCR acceleration compared to GMRES
acceleration can be significant. The only difference with GMRES is
that GCR needs some additional vector updates and requires some
more memory. A more efficient implementation, see [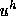 of the Poisson equation
with the exact solution
of the Poisson equation
with the exact solution 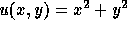 .
.
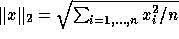 .
Clearly, the solutions obtained with both algorithms have approximately
the same accuracy. Only for large subdomain accuracy (giving very
large computing time) the algorithm for accurate solution of subdomains
gives a more accurate solution.
This verifies our earlier claim that the solution obtained with
GMRES acceleration used with accurate solution
of subdomains is sensitive to the subdomain solution accuracy.
This sensitivity is not present with the GCR based acceleration procedure
used with inaccurate solution of subdomains.
.
Clearly, the solutions obtained with both algorithms have approximately
the same accuracy. Only for large subdomain accuracy (giving very
large computing time) the algorithm for accurate solution of subdomains
gives a more accurate solution.
This verifies our earlier claim that the solution obtained with
GMRES acceleration used with accurate solution
of subdomains is sensitive to the subdomain solution accuracy.
This sensitivity is not present with the GCR based acceleration procedure
used with inaccurate solution of subdomains.
