CFD is a major discipline in which one tries to predict the behaviour all sorts of flows by numerical means. With the tremendous increase in computer technology and the development of efficient numerical algorithms, one aims at computing flows. More specifically, the focus is towards gas dynamics.
There are two main advantages of unstructured grids over structured grids: grid generation can be performed with a drastic reduction of man labor, and local and adaptive grid refinement are much easier to realize.
In our research we restricted ourselves to 2D grids consisting of triangles, as shown in the present figure of a grid around a NACA0012 airfoil.

Loosely speaking, in a flow in which the Mach number remains uniformly low (say, lower than 0.2), density variations may be neglected and the flow can be considered as incompressible. On the other hand, if the Mach number in the flow is everywhere larger than the aforementioned value, then the flow has to be considered as compressible. Because of the differences in the mathematical behavior of these two flow types, compressible and incompressible CFD have largely gone their own way. However, in real-life applications such type of flows does occur. Just to name some examples, during landing and take-off of an aircraft, in the wake behind re-entry vehicles, or in cavitating flows.
At this moment, the developed unstructured methodology is capable of computing both compressible and incompressible flows, while using the same spatial discretization and solver strategy, and without loss of accuracy or efficiency. We will show some numerical results immediately below.
A well-known testcase in which an incompressible flow (Mach = 0) is involved, is the backward facing step. The streamlines for a Reynolds number equal to 389 are depicted in the figure included below. A central scheme is used to treat the convection term.

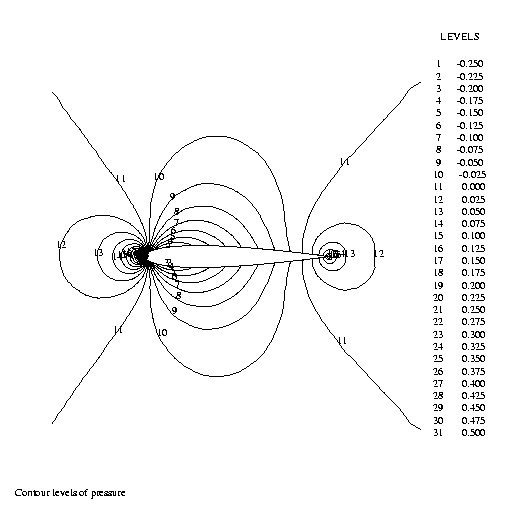
The isobars of a flow in the low subsonic regime (Mach = 0.1) around a NACA0012-profile, with zero angle of incidence, are demonstrated here.
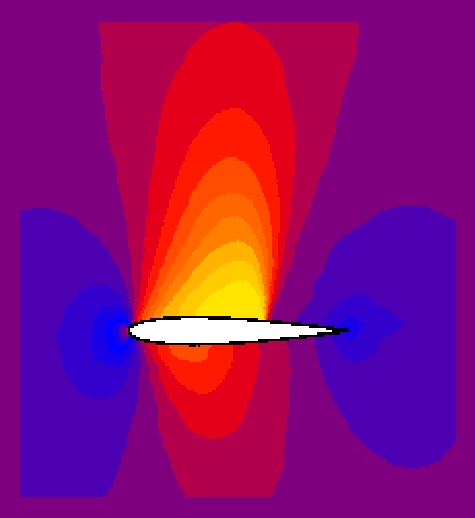
A picture demonstrating results of a testcase in which a transonic flow is involved, is shown below. The Mach number around a NACA0012-airfoil, with freestream Mach number equal to 0.8 and flow angle of attack 1.25, is demonstrated. The first order upwind scheme has been used to compute this results (see also Current status of the project).
An example in which incompressible and compressible flows, both occupying a large part of the domain, are present, is the flow in a converging-diverging nozzle that is shown below. The contraction ratio between inlet and throat height equals 20. The Mach number near the inlet equals 0.045, and the flow becomes supersonic after the throat, with a Mach number increasing up to 2.7.

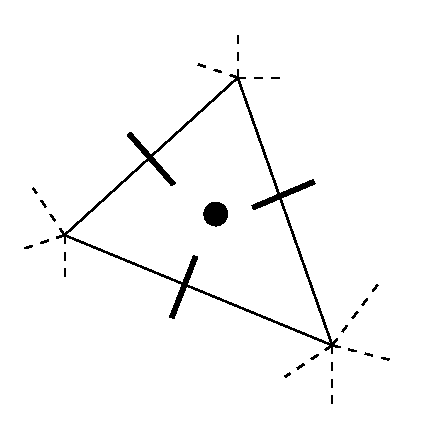
The scalar variables (pressure, density, total enthalpy, and so on) are stored in the centroids of the triangles, whereas the normal components of the momentum (velocity times density) are located at the midpoints of the cell faces. This is indicated in the figure. In literature, we have found only a few references to papers using an identical staggered arrangement on unstructured grids. A staggered grid arrangement, while not uncommon in incompressible CFD (see below), is rarely encountered in compressible CFD. Using a staggered grid is the most straightforward way to avoid odd-even decoupling in the pressure. Odd-even decoupling in the pressure is an undesired effect of discretization of the incompressible flow equations on colocated grids. Such a decoupling does not occur in the compressible case, explaining why there is no principal necessity to use staggered grids for compressible flows.
Because of the staggered positioning of the variables, one cannot apply Riemann solvers, commonly used in compressible CFD. Instead, a segregated solution procedure is adopted, in which each variable is updated sequentially. First order upwinding or central differencing is used to treat the convective terms. Such a procedure is often adopted in incompressible CFD, or in the field of shallow water equations. For more remarks concerning the spatial discretization, we refer to the papers.
Implicit methods (e.g. Euler backward) are used to do the time-stepping. Time-stepping in done in the `physical' time-domain only, hence both steady as unsteady problems can be dealt with. The linear systems resulting from the implicit time integration are solved by GMRES or Bi-CGSTAB, preconditioned with ILU (for the pressure equation) or ILUD (for the other equations).
Since the considered system of equations is coupled, this coupling has to be taken into account in some way when computing solutions. As stated above, a segregated solution procedure is adopted. For the compressible case, it turned out that this could be done in a straightforward manner. In the incompressible situation, in which no explicit equation for the pressure is available, the pressure-correction method is employed.
As stated above, the question remains what to do if a flow contains both compressible as incompressible parts. Most approaches start by taking the incompressible limit of the compressible equations in some appropriate manner. The immediate consequence is, that, among all other problems, the aforementioned odd-even decoupling can crop up, because a colocated positioning of the variables is employed. The approach that we are following, is basically the opposite, since we have started from the incompressible, staggered grid, approach. Avoiding the accuracy and efficiency problems that one encounters when dealing with low Mach number flow is done by using an appropriate non-dimensionalization of the pressure and derivation of a suitable pressure-correction algorithm.