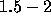In [7,8] parallelization of domain decomposition for the incompressible Navier-Stokes equations using accurate solution of subdomain problems is investigated. The method performs well on a cluster of workstations. The reason is that with accurate solution of subdomain problems the parallelization is rather coarse grained. Furthermore, the reduction to a system of interface equations (19) makes a very simple parallel implementation possible.
In this section, we take a brief look at the possibilities for parallel
implementation of the GCR accelerated method of this paper.
Table 5 shows a comparison between the
multiplicative and additive algorithms.
We see that the penalty of
going from the multiplicative to the additive algorithm is between
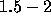for method II, which is more than for method III.
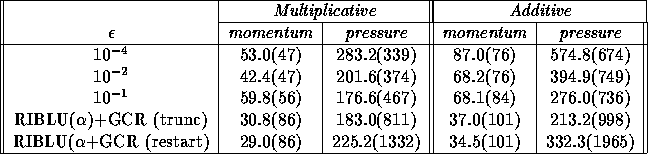
Table 5: Comparison between the multiplicative (Gauss-Seidel) and
additive (Jacobi) algorithm for
a decomposition into 8 blocks.
Table 5 shows that the number of iterations only increases
slightly as the subdomain solution accuracy is lowered to 
.
This means that lowering the subdomain accuracy will almost certainly
give a lower computing time.
Method III requires much more iterations, especially for the pressure
equations, and therefore communication.
Therefore, method II is more suitable for parallel
processing than method III. Again GCR with Jackson & Robinson truncation is
quite effective for method III compared to optimized restarted GCR.
The results in Table 5 show that for this problem, the multiplicative algorithm is more sensitive to the subdomain solution accuracy than the additive algorithm, probably because errors made in solving subproblems propagate to other subdomains within a single iteration.