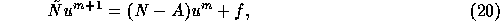
Domain decomposition iteration (10) is typically implemented as
where the right-hand side term 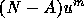 represents the discretization
of the internal boundary conditions, which is always exact, and
the left-hand side term
represents the discretization
of the internal boundary conditions, which is always exact, and
the left-hand side term 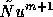 indicates solution of
the subdomain problems using some type of solver, which was assumed accurate
enough in the previous section.
indicates solution of
the subdomain problems using some type of solver, which was assumed accurate
enough in the previous section.
In general, the stationary solution of (20) satisfies
the perturbed equations 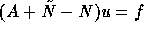 instead of Au = f.
Since with inaccurate subdomain solution, the difference between
instead of Au = f.
Since with inaccurate subdomain solution, the difference between
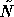 and N may be quite large, the computed solution u
may have a very large error. Since the algorithm of the previous section
relies on (20), we may not use this
procedure with inaccurate
solution of subdomain problems. Instead we must use
and N may be quite large, the computed solution u
may have a very large error. Since the algorithm of the previous section
relies on (20), we may not use this
procedure with inaccurate
solution of subdomain problems. Instead we must use
for which the stationary solution u always satisfies Au = f.
With inaccurate subdomain solution, we have
with 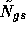 the Gauss-Seidel (sequential/multiplicative) version and
the Gauss-Seidel (sequential/multiplicative) version and
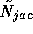 the Jacobi (parallel/additive) version of
the Jacobi (parallel/additive) version of 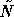 .
The matrices
.
The matrices 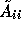 represent inaccurate subdomain solution.
The matrix vector product
represent inaccurate subdomain solution.
The matrix vector product 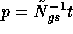 is computed like
is computed like
where, for instance, 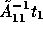 represents an approximate
solution in subdomain 1 with a low accuracy.
Another possibility is to take
represents an approximate
solution in subdomain 1 with a low accuracy.
Another possibility is to take
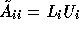 to be some incomplete LU factorization
of
to be some incomplete LU factorization
of 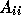 , see further on.
, see further on.
The GMRES subdomain solution implicitly constructs a polynomial 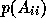 of the subdomain matrix
of the subdomain matrix 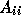 such that the final residual
such that the final residual
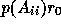 is minimal in the Euclidean norm. Specifically, with
initial guess
is minimal in the Euclidean norm. Specifically, with
initial guess 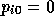 and right-hand side
and right-hand side 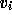 , we get for the final
subdomain solution
, we get for the final
subdomain solution 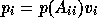 .
Since the polynomial
.
Since the polynomial 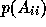 depends on both the required accuracy
and the right-hand side (initial residual), the matrix
depends on both the required accuracy
and the right-hand side (initial residual), the matrix
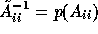 can be different for each v.
Therefore, GMRES acceleration cannot be used since
the preconditioner
can be different for each v.
Therefore, GMRES acceleration cannot be used since
the preconditioner 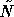 varies in each step. Only for the case
varies in each step. Only for the case
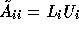 we may apply GMRES acceleration, but we still apply
GCR in this case.
we may apply GMRES acceleration, but we still apply
GCR in this case.