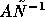 confirms this statement.
For symmetric
problems, the condition number is a good estimate for the rate of convergence
(
confirms this statement.
For symmetric
problems, the condition number is a good estimate for the rate of convergence
(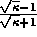 for CG) For
unsymmetric problems the condition number is less closely linked to
convergence.
for CG) For
unsymmetric problems the condition number is less closely linked to
convergence.
Inaccurate solution of subproblems reduces the amount of work in each domain decomposition iteration at the cost of some additional work in the outer domain decomposition iteration. Therefore this approach can only lead to a reduction in computing time if the increase in outer domain decomposition iterations is small.
A simple analysis of the condition number of the postconditioned matrix
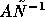 confirms this statement.
For symmetric
problems, the condition number is a good estimate for the rate of convergence
(
confirms this statement.
For symmetric
problems, the condition number is a good estimate for the rate of convergence
(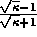 for CG) For
unsymmetric problems the condition number is less closely linked to
convergence.
for CG) For
unsymmetric problems the condition number is less closely linked to
convergence.
Each iteration involves solving
with N the matrix from (10). With inaccurate solution of subdomains, we solve a problem
with 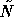 as in (22) and (21).
All subproblems are solved using a relative accuracy.
as in (22) and (21).
All subproblems are solved using a relative accuracy.
Theorem 1 relates N and 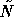 .
.
Proof:
Proof of (a): Combination of Condition 1 with(inaccurate subdomain solution) gives
for all
. From the definition of a matrix norm it follows that
.
Without loss of generality we take two subdomains, so that N andare described by (15) and (22) respectively. We get
Partition
and note that for the Euclidean norm
, then we have
.
Furthermore, for the Euclidean normimplies
and
so that finally (a) follows with
.
Proof of (b): For any block diagonal matrix, we have:
. If we use the additive postconditioner, then
is a block diagonal matrix with blocks
, so that
. Therefore, (b) holds.

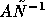 and
and 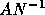 .
.
Proof:
Application of Theorem 1, and noting thatis a least upper bound norm, gives
and
.
Since,
.
Inequality (27) follows from.

Theorem 2 shows that the subdomain solution accuracy has
only a small effect on the condition number of the postconditioned matrix.
This means that (at least for symmetric problems) the number of outer
iterations will not increase (significantly) when the subdomain accuracy is
lowered.
The sensitivity of outer loop convergence to  is given
by the constant C in Theorem 1, which can be chosen
1 for the additive algorithm, independently of the number of subdomains.
For multiplicative algorithms this sensitivity constant C will probably
also be small and independent of the number of subdomains, however, sharper
bounds may require a much more detailed analysis.
is given
by the constant C in Theorem 1, which can be chosen
1 for the additive algorithm, independently of the number of subdomains.
For multiplicative algorithms this sensitivity constant C will probably
also be small and independent of the number of subdomains, however, sharper
bounds may require a much more detailed analysis.
The theorems only hold for constant 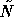 , but the results
in Section 6 show that the conclusions also hold
in case
, but the results
in Section 6 show that the conclusions also hold
in case 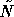 varies in each iteration.
varies in each iteration.