


Next: The model problem
Up: Domain decomposition for the
Previous: Theoretical motivation
The basic Schwarz domain decomposition iteration converges slowly and is
not always convergent for the Navier-Stokes equations.
Therefore, we use Krylov subspace acceleration, which is
frequently used to accelerate domain decomposition methods, see for example
[5] and many of the papers on iterative substructuring
methods in [24,14,15,25,33].
The acceleration procedure used with accurate solution of subdomain problems
is GMRES applied to the interface equations (19) and is
described in detail in [11,10].
This section describes the procedure used with inaccurate subdomain solution.
The GCR [23] method for solving Ax = f
can be easily adapted to cope with
variable preconditioners. Because of its simplicity and for
completeness, we describe the GCR
method here. GCR is based on maintaining two
subspaces, a subspace 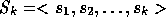 for storing the
search directions
for storing the
search directions 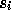 and a subspace
and a subspace
 with
with 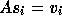 . In every operation
of GCR the property
. In every operation
of GCR the property 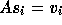 is preserved.
For simplicity we take the initial guess
is preserved.
For simplicity we take the initial guess  , in which case
GCR minimizes the residual
, in which case
GCR minimizes the residual
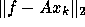 over
over 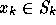 . Clearly, if the
. Clearly, if the 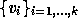 form an orthonormal basis, we can obtain the solution by projecting onto
the space
form an orthonormal basis, we can obtain the solution by projecting onto
the space 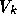 . So we must find
. So we must find 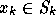 such that
such that
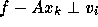 for
for 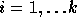 , therefore,
, therefore,

Since 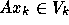 we have
we have

and by substituting (29)
into (28)
we get 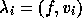 so that
so that

Since 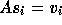 , we have
, we have
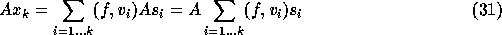
so that 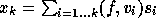 .
This gives
.
This gives 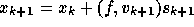 and
with
and
with  we get
we get
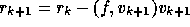 .
The GCR algorithm proceeds by choosing a new search direction
.
The GCR algorithm proceeds by choosing a new search direction 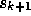 (preferably such that
(preferably such that 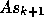 approximates the residual
approximates the residual  ) and computes the vector
) and computes the vector
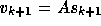 . A modified Gram-Schmidt procedure is used to
make
. A modified Gram-Schmidt procedure is used to
make  orthogonal to
orthogonal to 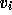 (
(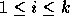 ). The same linear
combinations of vectors are applied to the space of search directions
). The same linear
combinations of vectors are applied to the space of search directions 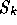 to ensure that
to ensure that 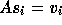 still holds for all i.
Figure 4 shows the resulting GCR algorithm.
still holds for all i.
Figure 4 shows the resulting GCR algorithm.

Figure 4: The GCR algorithm with general search directions without
restart and with a relative stopping criterion [46]
For the special case of the search direction 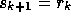 , we
obtain the classical GCR algorithm, which is equivalent to GMRES [41].
For this choice of search direction, the space
, we
obtain the classical GCR algorithm, which is equivalent to GMRES [41].
For this choice of search direction, the space  is called the
Krylov space. The difference between GCR and GMRES is that, with the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and
is called the
Krylov space. The difference between GCR and GMRES is that, with the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and 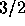 times the number of floating
point operations for orthogonalization.
However, GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [31] strategy,
whereas GMRES can only be restarted. Because of this, truncated GCR may converge
faster than GMRES, see for example Section 6.2.
Furthermore, restarted GCR can be optimized [49],
which makes GCR just as efficient as GMRES. Both optimized restarted
GCR and truncated GCR will be considered in our numerical experiments.
times the number of floating
point operations for orthogonalization.
However, GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [31] strategy,
whereas GMRES can only be restarted. Because of this, truncated GCR may converge
faster than GMRES, see for example Section 6.2.
Furthermore, restarted GCR can be optimized [49],
which makes GCR just as efficient as GMRES. Both optimized restarted
GCR and truncated GCR will be considered in our numerical experiments.
Recent developments have led to a more flexible GMRES algorithm
which allows more general search directions, so called FGMRES [40].
The FGMRES method is used in [6] to investigate the Neumann-Dirichlet
method with inexact subdomain solution. The emphasis in [6] is
on restrictions on subdomain solution accuracy to retain the h-independent
convergence of the Neumann-Dirichlet algorithm rather than on reduction of
computing time.
Optimized restarted GCR is just as efficient as FGMRES, both in memory
requirements and work.
In the present paper, we use 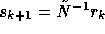 , which corresponds
to a single iteration of (21) with initial guess
, which corresponds
to a single iteration of (21) with initial guess 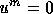 .
The case of multiple iterations of (21) to determine
.
The case of multiple iterations of (21) to determine 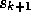 is not considered in this paper.
If the subdomain problems are solved (inaccurately) using GMRES, this method reduces
to GMRESR [46]
for the single domain case.
In case
is not considered in this paper.
If the subdomain problems are solved (inaccurately) using GMRES, this method reduces
to GMRESR [46]
for the single domain case.
In case 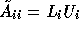 is the (relaxed) incomplete LU factorization of
is the (relaxed) incomplete LU factorization of
 , we obtain a blocked version of the subdomain RILU(
, we obtain a blocked version of the subdomain RILU( ) [27]
postconditioner (with parameter
) [27]
postconditioner (with parameter  ), here
called RIBLU(
), here
called RIBLU( ) (Relaxed Incomplete Block LU). The parameter
) (Relaxed Incomplete Block LU). The parameter  may be varied to improve convergence.
The RIBLU(
may be varied to improve convergence.
The RIBLU( ) preconditioner is investigated for parallel
implementation in for example [21,32,18,19].
The present paper also investigates the multiplicative version of the
RIBLU(
) preconditioner is investigated for parallel
implementation in for example [21,32,18,19].
The present paper also investigates the multiplicative version of the
RIBLU( ) postconditioner.
The GMRES acceleration procedure may be applied with RIBLU(
) postconditioner.
The GMRES acceleration procedure may be applied with RIBLU( ), which is
equivalent to GCR acceleration in this case.
), which is
equivalent to GCR acceleration in this case.
The stopping criterion for accurate solution of subdomain problems
differs from that for inaccurate solution. With accurate solution,
the stopping criterion is based on the preconditioned residual
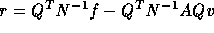 of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult.
Nevertheless, we assume that the final
solution obtained with both methods is equally accurate if the
relative stopping criterion
of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult.
Nevertheless, we assume that the final
solution obtained with both methods is equally accurate if the
relative stopping criterion 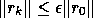 is used.
This assumption was confirmed in [9].
With inaccurate subdomain solution, the results for different subdomain
solution accuracies can be compared since the stopping criterion does
not depend on the way subdomain problems are solved.
is used.
This assumption was confirmed in [9].
With inaccurate subdomain solution, the results for different subdomain
solution accuracies can be compared since the stopping criterion does
not depend on the way subdomain problems are solved.



Next: The model problem
Up: Domain decomposition for the
Previous: Theoretical motivation
ISNaS ontwikkeling
Thu Jun 1 11:07:52 METDST 1995
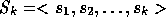 for storing the
search directions
for storing the
search directions 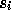 and a subspace
and a subspace
 with
with 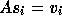 . In every operation
of GCR the property
. In every operation
of GCR the property 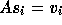 is preserved.
For simplicity we take the initial guess
is preserved.
For simplicity we take the initial guess  , in which case
GCR minimizes the residual
, in which case
GCR minimizes the residual
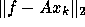 over
over 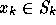 . Clearly, if the
. Clearly, if the 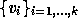 form an orthonormal basis, we can obtain the solution by projecting onto
the space
form an orthonormal basis, we can obtain the solution by projecting onto
the space 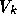 . So we must find
. So we must find 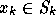 such that
such that
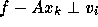 for
for 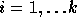 , therefore,
, therefore,

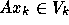 we have
we have

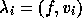 so that
so that

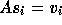 , we have
, we have
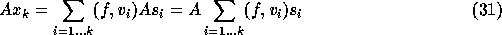
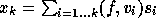 .
This gives
.
This gives 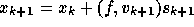 and
with
and
with  we get
we get
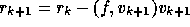 .
The GCR algorithm proceeds by choosing a new search direction
.
The GCR algorithm proceeds by choosing a new search direction 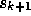 (preferably such that
(preferably such that 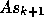 approximates the residual
approximates the residual  ) and computes the vector
) and computes the vector
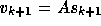 . A modified Gram-Schmidt procedure is used to
make
. A modified Gram-Schmidt procedure is used to
make  orthogonal to
orthogonal to 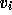 (
(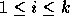 ). The same linear
combinations of vectors are applied to the space of search directions
). The same linear
combinations of vectors are applied to the space of search directions 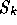 to ensure that
to ensure that 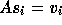 still holds for all i.
Figure
still holds for all i.
Figure 
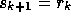 , we
obtain the classical GCR algorithm, which is equivalent to GMRES [
, we
obtain the classical GCR algorithm, which is equivalent to GMRES [ is called the
Krylov space. The difference between GCR and GMRES is that, with the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and
is called the
Krylov space. The difference between GCR and GMRES is that, with the
benefit of allowing more general search directions, GCR requires
twice the storage of GMRES and 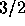 times the number of floating
point operations for orthogonalization.
However, GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [
times the number of floating
point operations for orthogonalization.
However, GCR can be combined with truncation
strategies, for instance the Jackson & Robinson [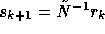 , which corresponds
to a single iteration of (
, which corresponds
to a single iteration of (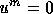 .
The case of multiple iterations of (
.
The case of multiple iterations of (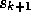 is not considered in this paper.
If the subdomain problems are solved (inaccurately) using GMRES, this method reduces
to GMRESR [
is not considered in this paper.
If the subdomain problems are solved (inaccurately) using GMRES, this method reduces
to GMRESR [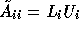 is the (relaxed) incomplete LU factorization of
is the (relaxed) incomplete LU factorization of
 , we obtain a blocked version of the subdomain RILU(
, we obtain a blocked version of the subdomain RILU( ) [
) [ ), here
called RIBLU(
), here
called RIBLU( ) (Relaxed Incomplete Block LU). The parameter
) (Relaxed Incomplete Block LU). The parameter  may be varied to improve convergence.
The RIBLU(
may be varied to improve convergence.
The RIBLU( ) preconditioner is investigated for parallel
implementation in for example [
) preconditioner is investigated for parallel
implementation in for example [ ) postconditioner.
The GMRES acceleration procedure may be applied with RIBLU(
) postconditioner.
The GMRES acceleration procedure may be applied with RIBLU( ), which is
equivalent to GCR acceleration in this case.
), which is
equivalent to GCR acceleration in this case.
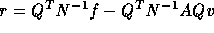 of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult.
Nevertheless, we assume that the final
solution obtained with both methods is equally accurate if the
relative stopping criterion
of
only the interface unknowns. On the
other hand, with inaccurate solution, it is based on the unpreconditioned
residual r = f - A u of all unknowns. Therefore, a comparison between
the two methods is difficult.
Nevertheless, we assume that the final
solution obtained with both methods is equally accurate if the
relative stopping criterion 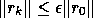 is used.
This assumption was confirmed in [
is used.
This assumption was confirmed in [