One of the main reasons for investigating inaccurate solution of subdomain problems is to reduce the excessive computing times observed in the multi-block incompressible Navier-Stokes solver [10], and to bring them closer to single-block solution time. This also gives better prospects for parallel computing.
Table 2 lists the number of iterations and computing times
for single-block solution of the Poisseuille flow on an 
grid
and the single-block cylinder grid with 10800 cells from Figure 5.
The results
are given for GMRES subdomain solution using
RILU(
) postconditioning.
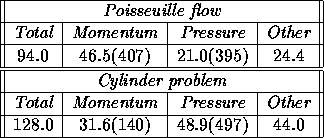
Table 2: Single-block solution using GMRES with RILU(
) postconditioning
Table 3 shows a comparison of single-block solution and multi-block solution of the momentum equations for different decompositions of the domain.
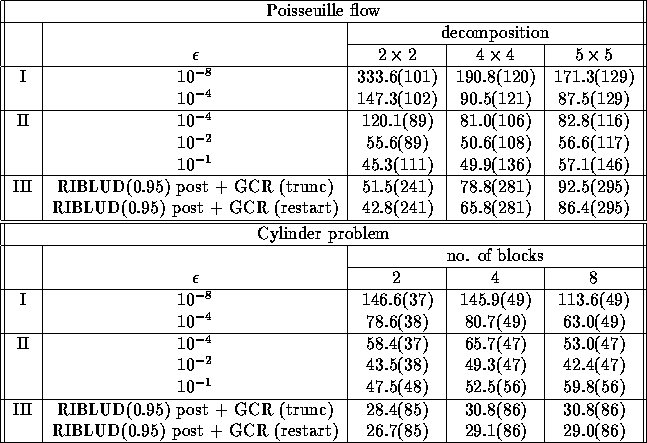
Table 3: Results with various decompositions into subdomains for the momentum
equations, multiplicative algorithm.
Table 4 shows a comparison of single-block solution and
multi-block solution of the pressure equations for different decompositions
of the domain. It is important to note that with the optimized restarted
GCR method with RIBLU(
) postconditioning (the bottom row in Table 4),
the maximum dimension of the Krylov space had to be increased to 40 to
obtain convergence within 200 iterations/time step of the pressure equation.
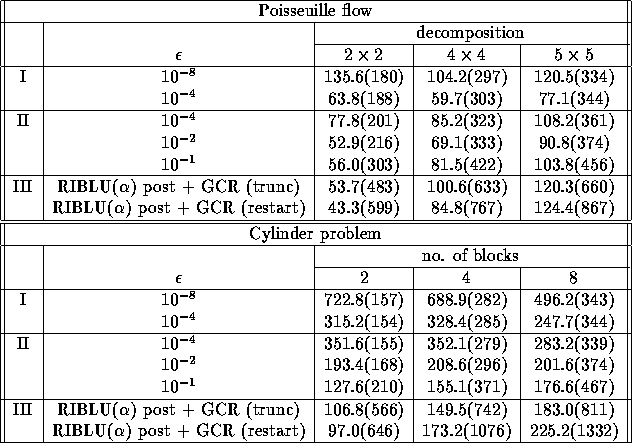
Table 4: Results with various decompositions into subdomains for the pressure
equations, multiplicative algorithm.
Comparing Tables 2 and 3, we see that
for small numbers of subdomains,
computing time for the momentum equations can be reduced to below
that of single-block solution for method II.
However, for larger numbers of blocks this is not the case, which is
possibly due to superlinear convergence of the subdomain solvers, see further
on.
Method III is faster than method II for the cylinder problem, but not for
the Poisseuille problem.
An explanation is that the time step for the cylinder problem
(
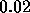) is much smaller than for the Poisseuille flow (
) which
increases the diagonal of the momentum matrix considerably and improves
convergence.
Comparing Tables 2 and 4, we see that
for small numbers of subdomains, the computing time with method II with
inaccurate subdomain solution is still a factor 2-3 larger than with single
block solution. Also, for the Poisseuille flow in Table 4
inaccurate subdomain solution does not always provide a speedup.
Method III leads to growing
iteration count and computing times for increasing numbers of blocks.
The reason for the bad performance of the RIBLU(
)
postconditioner is that for 
close to 
, it performs much worse
with respect to single domain RILU(
) than for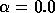 
,
see Section 6.3.
We also see that the Jackson & Robinson truncation strategy is quite
effective in reducing iteration count compared to restarted GCR.
The optimizations in GCR do not outweigh this increase in iteration count.
A possible reason for the modest reduction in computing time by method II
for larger numbers of blocks is the following. For larger numbers of blocks
the subdomains are smaller and therefore superlinear convergence of the
subdomain GMRES solver can occur earlier. For example, in case of superlinear
convergence,
lowering the subdomain solution accuracy from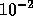 
to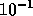 
might
only save a single subdomain GMRES iteration (out of say 6 iterations).
The subdomain solution accuracy therefore only gives a small reduction
of work needed to solve subdomains, but it may still cause a significant
increase in the number of GCR iterations in the outer loop.
The results in Table 3 and Table 4
confirm the remark in Section 3.4 that the
constant C in Theorem 2 does not depend on
the number of blocks for the multiplicative algorithm:
the ratio of the number of iterations needed
with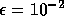 
and 
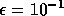does not increase as the
domain is decomposed into more subdomains.