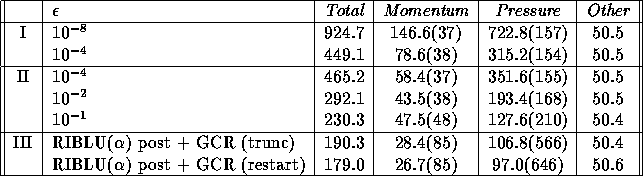
Table 1: Results with varying accuracy of subdomain solution for the cylinder problem, multiplicative algorithm
Table 1 lists the computation times and iteration counts for the cylinder problem. A decomposition into two blocks is used as in Figure 5.a. The table shows the following quantities:
 ) preconditioner to the subdomain right-hand side.
) preconditioner to the subdomain right-hand side.

Table 1: Results with varying accuracy of subdomain solution for the cylinder
problem, multiplicative algorithm
As the subdomain solution accuracy is lowered from 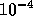 to
to 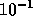 ,
the number of outer GCR
iterations shows only a small increase, which, because of the reduced work
in solving subproblems, results in a reduction
of total computing time (here approximately a factor two).
This is in accordance with Theorem 2.
,
the number of outer GCR
iterations shows only a small increase, which, because of the reduced work
in solving subproblems, results in a reduction
of total computing time (here approximately a factor two).
This is in accordance with Theorem 2.
The use of the RIBLU( )
postconditioner (method III) leads to small amounts of work per iteration at the
cost of much larger iteration counts. The computing time is somewhat
lower than for method II.
This is contrary to our model study for
the advection-diffusion equation [9], where the RIBLU(
)
postconditioner (method III) leads to small amounts of work per iteration at the
cost of much larger iteration counts. The computing time is somewhat
lower than for method II.
This is contrary to our model study for
the advection-diffusion equation [9], where the RIBLU( )
postconditioner
resulted in a more significant drop in computing time. The reason is that
RIBLU(
)
postconditioner
resulted in a more significant drop in computing time. The reason is that
RIBLU( ) preconditioner shows a larger increase in number iterations
with respect to subdomain RILU(
) preconditioner shows a larger increase in number iterations
with respect to subdomain RILU( ) for
) for  close to
close to 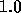 .
This increase is not present with
.
This increase is not present with 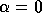 , see [9] and
Section 6.3.
The use of optimized restarted GCR instead of Jackson & Robinson truncation
gives only a
small reduction in computing time. For the momentum equations the total
number of iterations is the same which is because the number of iterations
per time step is below 20: the dimension of the Krylov space.
, see [9] and
Section 6.3.
The use of optimized restarted GCR instead of Jackson & Robinson truncation
gives only a
small reduction in computing time. For the momentum equations the total
number of iterations is the same which is because the number of iterations
per time step is below 20: the dimension of the Krylov space.