Numerical methods for large algebraic systems
(wi4010)
- The course is scheduled in the period: February 7 until March
25, 2005
Monday 13.45-15.30 room: G Mekelweg 4
Thursday 15.45-17.30 room: G Mekelweg 4
- The
lecture notes are only available in
electronic form.
- Lectures
-
Practical exercises and
the required matlab files in a
zip
or in a
tar
document
- Matlab implementation
of the algorithms presented in the lecture notes.
- Historical remarks
-
Disasters caused by numerical errors
- Related
information
applications,
disasters caused by numerical errors,
books, software packages etc.
-
Blackboard
Numerical methods for large algebraic systems (wi4010)
After some introduction
direct methods are presented to solve large (sparse) linear systems.
The origin of these systems are in general discretized partial
differential equations. For the directs method much emphasis is
given to calculate the results in a stable way with respect to
rounding errors. Depending on the properties of the matrices
various optimized methods are available as there are:
Choleski decomposition for symmetric and positive definite matrices,
sparse matrix methods for matrices containing a small number
of non-zero elements per row, band methods for band matrices etc.
Many problems in real life lead to least squares problems. Some
methods to solve them together with rounding error analysis are
specified. Finally iterative method to solve large linear systems
of equations are given. We start with simple Gauss Jacobi,
Gauss Seidel, continue with more advanced Chebyshev methods
and end with the Conjugate Gradient method. Some remarks concerning
the convergence of the CG method are given. For the CG method
some preconditioning methods are mentioned to accelerate the
convergence.
Some historical remarks concerning mathematicians, which name or work
is used in this course, are given on this
page
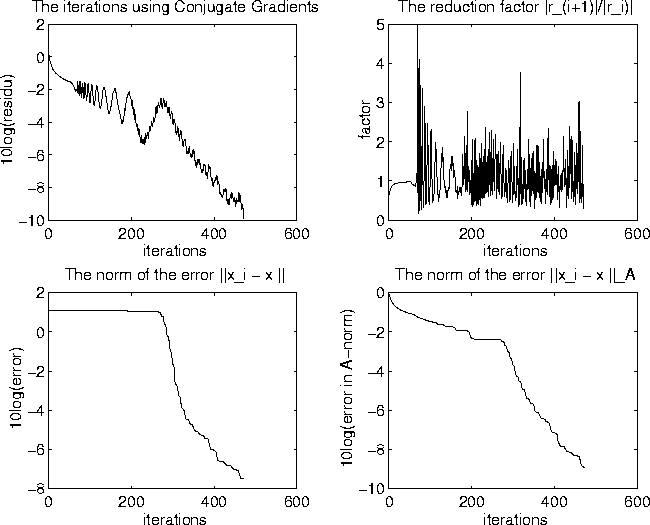
As an example
the convergence behaviour of the
CG method for a bending beam problem is given.

Information related to wi4010: Advanced course on numerical linear
algebra
Applications
Below a list is given of projects where numerical linear algebra is
used:
Rounding errors
In general it is difficult to get a good analysis of rounding errors
due to floating point arithmetic done by computers. To motivate the
study of rounding errors we note that several
disasters are originated by rounding errors. Recent examples are:
Patriot Missile Failure and the
Explosion of the Ariane 5.
Numerical errors
The sinking of the
Sleipner A offshore platform has been caused by
inaccurate finite element approximation of the linear elastic model of
the
tricell (using the popular finite element program NASTRAN).
The shear stresses were underestimated by 47%, leading to insufficient
design.
Some interesting links to obtain information or
software for numerical linear algebra
problems are:
- EnVision
The San Diego Supercomputer Center
is a large laboratory for
computational science and engineering. The publish a quarterly journal
enVision
which contains nice papers on computational science.
- Linux Software Encyclopedia
Linux Software Encyclopedia
is an alphabetized and annotated list of links to various
software amenable to installation and use on computers running the
Linux operating system.
- Matlab
The MathWorks, Inc. was established in December, 1984 to develop and
market interactive engineering and scientific software products. We
specialize in providing high-performance numeric computation and
graphics in an easy-to-use environment for university, government, and
commercial markets, worldwide. Our main product,
MATLAB, has become
the de facto standard for numeric computation among engineering and
scientific users.
- NAG
The Numerical Algorithms Group
(NAG) is a Not For Profit software house.
We specialise in the research and development of Scientific and
Technical
software. From the early days we have been producing high quality
software that is robust, reliable and portable across a wide range of
hardware, from the smallest PC to the most modern supercomputers.
- Netlib
In the
netlib library many software packages are available
to solve linear algebra problems.
Below we give some of the most interesting entries:
BLAS
BLAS (Basic Linear Algebra Subprograms) contains
subroutines to
calculate inner products, matrix vector products etc. A quick reference
guide is available.
LAPACK
LAPACK
provides routines for solving systems of simultaneous linear
equations, least-squares solutions of linear systems of equations,
eigenvalue problems, and singular value problems.
Templates package
It is possible to obtain the SIAM
book "Templates for the solution of linear systems" as a ps-file.
Click on the templates/templates.ps link at the
templates index page.
- Octave
Octave
is a high-level interactive language primarily for numerical
computations which is mostly compatible with Matlab. It can do
arithmetic for real and complex scalars and matrices, solve sets
of nonlinear algebraic equations, integrate functions over finite
and infinite intervals, and integrate systemes of ordinary
differential and differential-algebraic equations.
- TOMS
Transactions on Mathematical Software
(TOMS) published by the
Association for Computing Machinery
(ACM) contains many useful
algorithms.
Other sources of mathematical software can be found
here.

Contact information:
Kees Vuik
Back to
home page or
educational page of Kees Vuik


![]()
![]()
![]()